Hallo Roland,
ich nehme an. Du willst auf folgendes hinaus:
Die Gesamtlänge für \(x=0\) lässt sich mit der Kenntnis von \(\sqrt{2}\gt 1,414\) abschätzen:$$ L(x=0) = 2 \cdot 10 \cdot \sqrt{2} \gt 20\cdot 1,414=28,28 $$und weiter kann man sich folgenden Fall vorstellen:
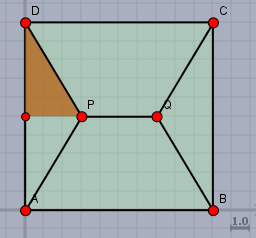
oben ist \(x=4\) womit sich ein \(L\) ergibt von:$$L(x=4) = 4 \cdot \sqrt{5^2 + 3^2} + 4 = 4(\sqrt{34}+1) \lt 4\cdot 6,831 = 27,324$$
daraus folgt:$$L(x=4) \lt L(x=0)$$demnach kann der Fall \(x=0\) nicht die kürzeste Gesamtlänge sein.
Ein geometrischer Ansatz:
In einem rechtwinkligen Dreieck, welches die Hälfte eines gleichseitigen Dreieck ist, betragen die WInkel \(30°\) (gelb) und \(60°\) (blau).
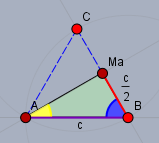
... und natürlich ist die rote Strecke genau halb so lang wie die lilane.
Mal angenommen, der Punkt \(P\) in obigem Bild ist so positioniert, dass der WInkel zwischen zwei benachbarten Straßen immer 120° ist. Wie verändert sich dann die Gesamtlänge \(L\), wenn man den Punkt \(P_{120°}\) in Richtung der Quadratmitte nach \(P^{-}\) verschiebt?
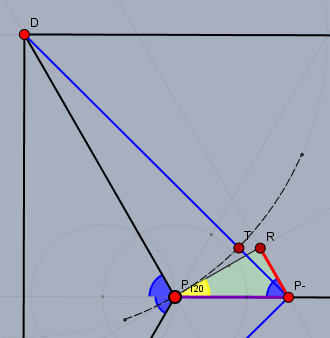
Das Straßenstück \(P_{120°}D\) wird um die Strecke \(TP^{-}\) länger. Und da \(T\) offensichtlich stets oberhalb der Geraden durch \(PR\) verläuft, gilt$$|TP^{-}| \gt |RP^{-}| = \frac{1}{2}|P_{120°}P^{-}|$$Da sich das symmetrische Stück \(AP^{-}\) in gleicher Weise verlängert und die Strecke \(x\) nur um \(|P_{12°}P^{-}|\) verkürzt wird, gilt demnach$$L(P^{-}) = L\left(P_{120°}\right) + 2\cdot TP^{-} - |P_{120°}P^{-}| \gt L\left(P_{120°}\right) + 2\cdot \left(\frac{1}{2}|P_{120°}P^{-}|\right) - |P_{120°}P^{-}| = L\left(P_{120°}\right)$$Verschiebt man \(P\) von \(P_{120°}\) aus nach links, so dass \(x\) größer wird, auf die Position \(P^{+}\), so sieht das so aus:
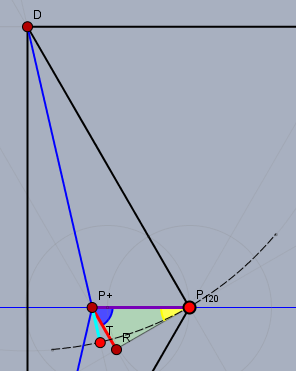
Hier verkürzt sich die Strecke \(|DP_{120°}|\) um den Betrag\(|P^{+}T|\). Und diese ist wiederum kleiner als \(|P^{+}R|\). Somit gilt$$L(P^{+}) = L\left({P_{120°}}\right) - 2|P^{+}T| + |P^{+}P_{120°}| \gt L\left({P_{120°}}\right) - 2\left(\frac{1}{2}|P^{+}P_{120°}|\right) + |P^{+}P_{120°}| = L\left({P_{120°}}\right)$$Folglich liegt im Punkt \(P_{120°}\) ein lokales Minimum für die Strecke \(L\) vor, was kleiner ist, als \(L(x=0)\). Her wären die Winkel jeweils \(90°\) und \(135°\).
Gruß Werner