Kann begründen, dass die gesuchten Punkte oberhalb eines Parabelbogens liegen?

Question

Ich hatte folgende Frage: "Man hat ein Dreieck (gleichschenklig!!!) XYZ mit der Basis [XY]. Auf den Seiten [XZ] und [YZ] wird ein Punkt T bzw. U so gesetzt, dass der Umfang von TUZ die Länge der Summe von XZ und ZY hat. Welche Punkte G im Dreieck drinnen können auf einer Strecke [TU] sein???"

Daraufhin habe ich eine Antwort in Form folgenden Bildes bekommen, jedoch keine genaueren Erläuterungen dazu (es fielen nur Worte wie "parabelbogen", was mir plausibel erschien):

 

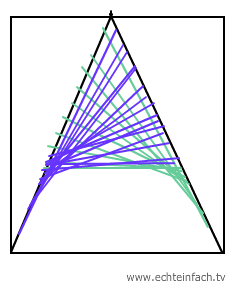
könnte mir jetzt irgendwer eine Erklärung oder einen Beweis geben, wie man darauf kommt? Wäre super, LG

Comments

Eine Begründung ist es nicht nur eine  zeichnerische Umsetzung der Aufgabenstellung.

Answer 1

Darüber habe ich auch schon nachgedacht. Das Bild ergibt sich einfach, wenn man auf der Strecke XZ einen Punkt P verschiebt und ihn über einen Punkt auf der Strecke YZ zu einem Dreieck mit dem Umfang XZ+YZ verbindet.

Die Frage ist nun, welche Form die weiße Fläche unten wirklich hat (auf den ersten Blick scheint parabolisch ein guter Tipp zu sein) und wie man das zeigt.

Eine Idee (zu der mir momentan die Zeit fehlt): man parametrisiere die Strecke PQ nach der x-Koordinate von P (denn dadurch ist sie bereits eindeutig festgelegt) und einen beliebigen Punkt darauf durch den Parameter t. Dann erhält man eine zweiparametrige Menge deren Struktur eigentlich irgendwie ersichtlich sein müsste.

Comments

Aus meinem Unterbewusstsein meldet sich übrigens das Wort Hyperbel, was deutlich plausibler als Parabel ist, weil ja zwei "Asymptoten" vorgegeben sind.

Falls noch irgendjemand gerade darüber nachdenkt :-)