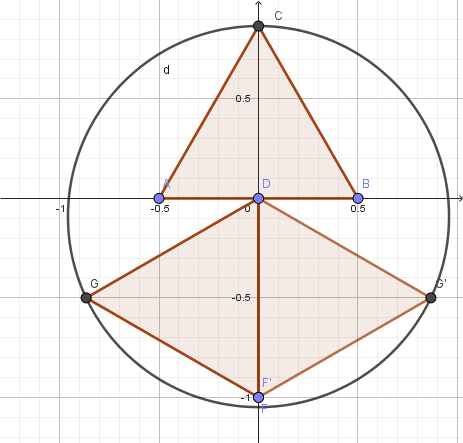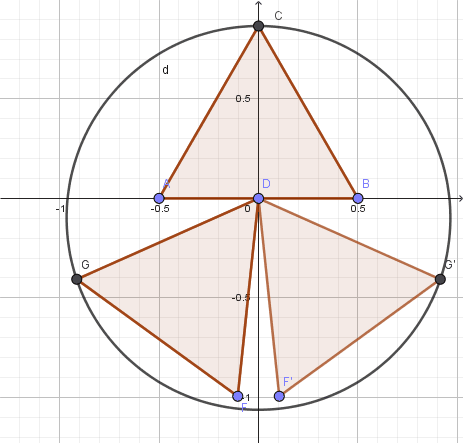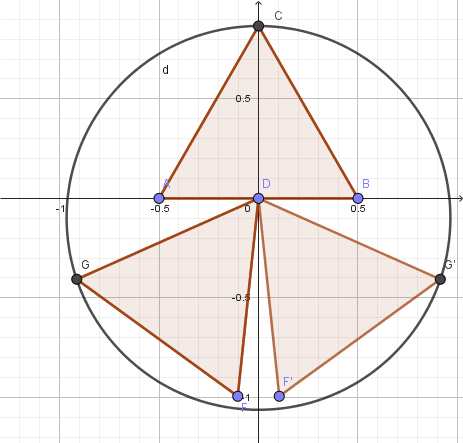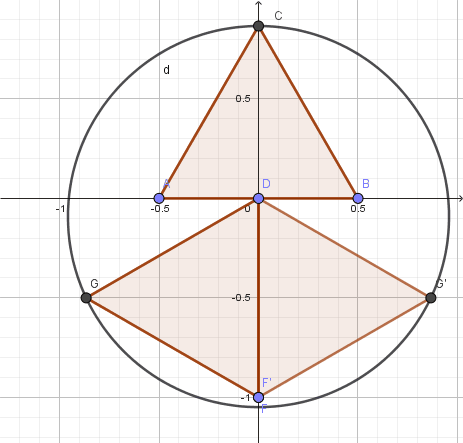
Wie ich richtig vermutet hatte ist der Umfang des Umkreises am kleinsten, wenn sich zwei Dreiecksseiten berühren.
In dieses Lage haben die 3 den Umkreis bestimmenden Eckpunkte die Koordinaten C(0|1), G(-0,5√3 | -0,5) und G'(0,5√3 | -0,5).
Da der sich daraus ergebende Kreis aber einen Radius >1 hat, gibt es bei der skizzierten Art der Anordnung keine Minimallage. Die Vermutung von willyengland ist richtig.