Diskriminate berechnen wie?

Question

Wie berechenet man wie der Parameter sein muss (k) dass es eine 2 oder keine Nullstelle gibt?

p(x)= x² + 3kx - k²

Ich weiß das man die Diskriminate benutzen muss

D = (3k)² - 4 * 1 * -k² 

D= 9k² +4k²

Aber weiter komm ich nicht, weiß jemand wie es da wieter geht

D>0 = zwei Nullstelle

D<0 = keine Nullstelle

Muss dan dan so aussehen zwei Nullstelle D = 9k² +4k² >0= Zwei Nullstelle?

Answer 1

D= (-1,5k)² +k² = 3,25k²

D ist immer größer oder gleich 0.

p(x) hat mindesten 1 Nullstelle.

Du hast die Diskriminante der abc-Formel verwendet. 9k²+4k² = 13k². D kann nicht negativ werden.

Comments

Ich verstehe nicht ganz deinen Ansatz was bedeutet dieses 3,25k^{2 .}

Bzw. Was sagt des zur Nullstelle aus?

---

Es gibt zwei oder eine.

D kann nicht negativ werden, es kann nicht keine Nullstelle geben.

---

Aber ich muss berechnen wann es gneuae 1 oder genau 2 Nullstelle hat also was k sein muss

---

Richtig.

----------------------------

---

Und bei kx² + 36x -k = 0 wenn man berechnen will das die Quadratische Gleichung nur eine Lösung hat muss man die Diskriminante 0 setzten aber bei dieser Aufgabe ist das egal was k ist denn es gibt immer 2 Lösungen oder?

Wäre meine Letze frage, danke für deine Geduld

Answer 2

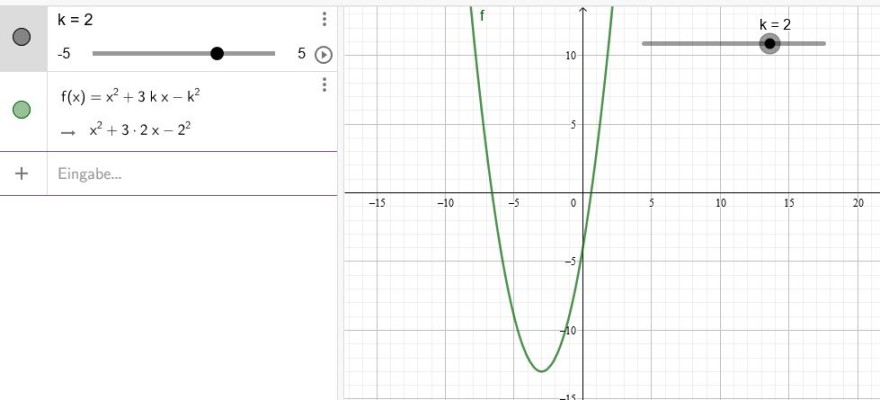
$p(x)= x^2 + 3kx - k^2$

$x^2 + 3kx - k^2=0$

$x^2 + 3kx =k^2$

$(x + 1,5k)^2 =k^2+(1,5k)^2=3,25k^2$

1.)

 $x + 1,5k=k*\sqrt{3,25}$

$x_1 =-1,5k+k*\sqrt{3,25}$

2.)

 $x + 1,5k=-k*\sqrt{3,25}$

$x_2 =-1,5k-k*\sqrt{3,25}$

Es gibt immer 2 Nullstellen. Bei $k=0$ hat du $p(x)= x^2$ Normalparabel.

Comments

Es gibt immer 2 Nullstellen. Bei $k=0$ hat du $p(x)= x^2$ Normalparabel.

Das widerspricht sich.

Für k=0 gibt es genau eine Nullstelle.

Für k≠0 gibt es zwei Nullstellen.

---

Ich sehe bei $f(x)=x^2$  die Stelle $x=0$ als doppelte Nullstelle an.