Lucas-Zahlen Beweis Induktion

Question

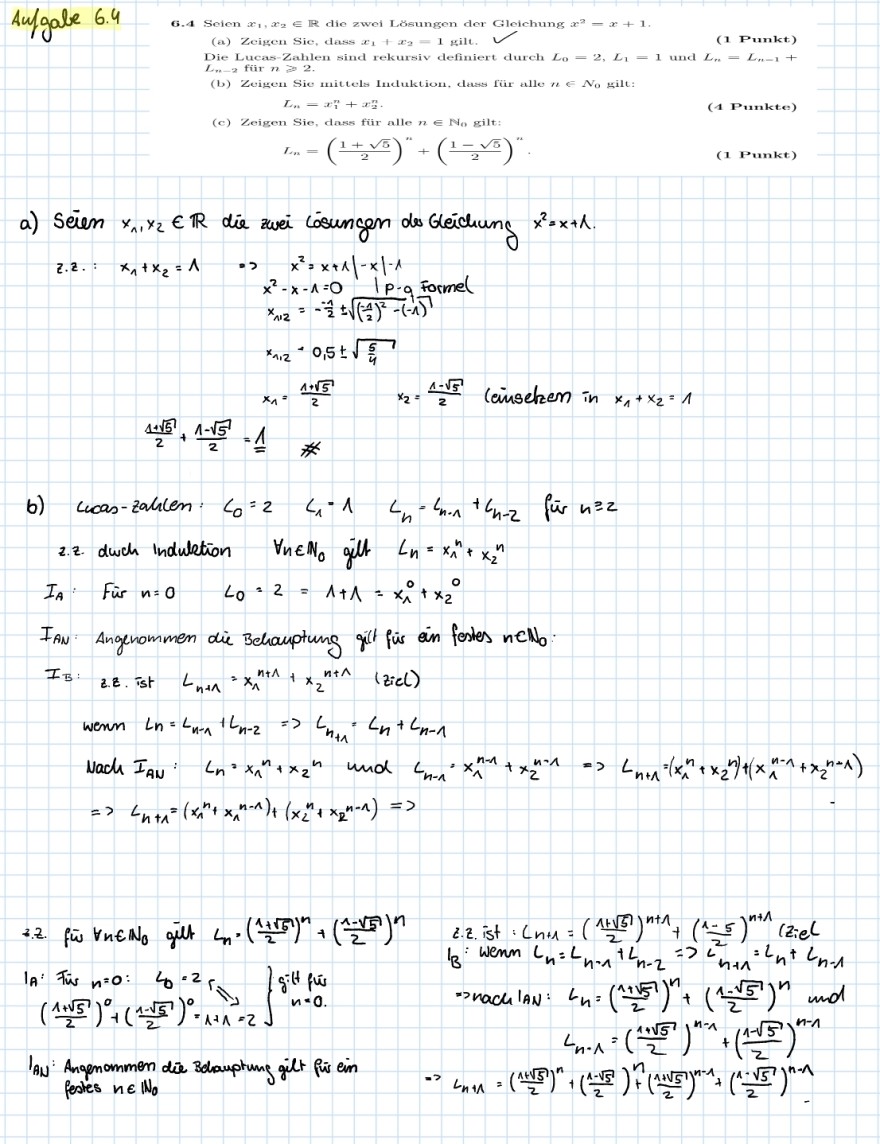
Text erkannt:

Aufgabe 6.4
6.4 Seien $x_{1}, x_{2} \in \mathbb{R}$ die zwei Lösungen dex Gleichung $x^{2}=x+1$
(a) Zeigen Sic, dess $x_{1}+x_{2}=1$ gilt.
(1 Punkt)
Die Lucas-Zahlen sind rekursiv definiert durch $L_{0}=2, L_{1}=1$ und $L_{n}=L_{n-1}+$
$L_{n-2}$ für $n \geqslant 2$.
(A Punktes)
$L_{n}=x_{1}^{n}+x_{2}^{n}$
(c) Zeigen Sie, dass fuir alle $n \in \mathbb{N}_{0}$ gilt:
$T_{n}=\left(\frac{1+\sqrt{5}}{2}\right)^{n}+\left(\frac{1-\sqrt{5}}{2}\right)^{n}$
(1 Punkt)
a) Seien $x_{1}, x_{2} \in \mathbb{R}$ die zwei lösungen des Gleichung $x^{2}=x+1$.
Z.z.:
$\begin{aligned} x_{1}+x_{2}=1 \quad \rightarrow \quad x^{2} & =x+1|-x|-1 \\ x^{2}-x-1 & =0 \quad \mid p-q \text { Formel } \\ x_{112} & =-\frac{11}{2} \pm \sqrt{\left(-\frac{1}{2}\right)^{2}-(-1)} \\ x_{1,2} & -0,5 \pm \sqrt{\frac{5}{4}} \\ & x_{1}=\frac{1+\sqrt{5}}{2} \quad x_{2}=\frac{1-\sqrt{5}}{2} \quad \text { ceiusetzen in } x_{1}+x_{2}=1 \\ \frac{1+\sqrt{5}}{2}+\frac{1-\sqrt{5}}{2}=1 & \end{aligned}$
b) cuas-zalicen: $c_{0}=2 \quad c_{1}=1 \quad c_{n}=c_{n+1}+c_{n-2}$ füs $n \geqslant 2$
z.z. dwch Indutetion $\forall n \in \mathbb{N}_{0}$ gill $L_{n}=x_{1}^{n}+x_{2}^{n}$
$I_{A}:$ Für $n=0 \quad L_{0}=2=1+1=x_{1}^{0}+x_{2}^{0}$
$I_{A N}:$ Angenommen die Behauptung gilt füs ain festes nello:
$I_{B}:$ z.z. ist $L_{n+1}=x_{1}^{n+1}+x_{2}^{n+1}$ (zicl)
wenn $L_{n}=L_{n-1}+L_{n-2} \Rightarrow L_{n+1}=L_{n}+L_{n-1}$
Nach $I_{A N}: L_{n}=x_{1}^{n}+x_{2}^{n}$ und $L_{n-1}=x_{1}^{n-1}+x_{2}^{n-1} \Rightarrow L_{n+1}=\left(x_{1}^{n}+x_{2}^{n}\right)+\left(x_{1}^{n-1}+x_{2}^{n+1}\right)$
$\Rightarrow L_{n+1}=\left(x_{1}^{n}+x_{1}^{n-1}\right)+\left(x_{2}^{n}+x_{2}^{n-1}\right) \Rightarrow$
$I_{A}: T_{\bar{\omega}} n=0: L_{0}=2 \quad \quad I_{B}:$ wenn $L_{n}=L_{n-1}+L_{n-2} \Rightarrow L_{n+1}=L_{n}+L_{n-1}$
$\Rightarrow$ nach $I_{A N}: L_{n}=\left(\frac{1+\sqrt{5}}{2}\right)^{n}+\left(\frac{1-\sqrt{5}}{2}\right)^{n}$ und
$L_{n-1}=\left(\frac{1+\sqrt{5}}{2}\right)^{n-1}+\left(\frac{1-\sqrt{5}}{2}\right)^{n-1}$

IAN: Angenommen die Bolauptung gilt fis ein festes $n \in \mathbb{N}_{0}$
$\Rightarrow L_{n+1}=\left(\frac{1+\sqrt{5}}{2}\right)^{n}+\left(\frac{1-\sqrt{5}}{2}\right)^{n}+\left(\frac{1+\sqrt{5}}{2}\right)^{n-1}+\left(\frac{1-\sqrt{5}}{2}\right)^{n-1} \text {. }$

An sich habe ich die Aufgabe ja schon fast gelöst, nur bin ich mir bei b und c nicht genau sicher, welche Potenzgesetze ich hier nun weiter verwenden kann, um mein Ziel zu erreichen? Hat jemand vielleicht eine Idee?

Answer 1

Hallo,

hat jemand vielleicht eine Idee?

Ja - verwende die Beziehung $x^2=x+1$$$\begin{aligned} L_{n+1} &= L_{n} + L_{n-1}\\ &= x_1^{n} + x_2^{n} + x_1^{n-1} + x_2^{n-1}\\ &= \left(x_1 + 1\right)x_1^{n-1} + \left(x_2 +1\right) x_2^{n-1}&& |\, x_{1,2}^2=x_{1,2}+1\\ &= x_1^2\cdot x_1^{n-1} + x_2^{2}\cdot x_2^{n-1}\\ &= x_1^{n+1} + x_2^{n+1}\\ &\text{q.e.d.} \end{aligned}$$Bem.: Im Induktionsanfang musst Du den Zusammenhang für zwei(!) auf einander folgende $n$ zeigen.

Bem2.; für a) reicht der Satz von Vieta oder auch ein Koeffizientenvergleich von$$\begin{aligned}x^2&=x+1 \\x^2-x-1 &= 0\\ (x-x_1)(x-x_2) &= 0 \\ x^2 - \underbrace{(x_1+x_2)}_{=1}x + x_1x_2 &=0 \end{aligned}$$es ist also nicht nötig, die Gleichung zu lösen.

Gruß Werner

Comments

Vielen Dank!!!

Das ist wirklich sehr hilfreich und nachvollziehbar. Tatsächlich hatte ich auch schon die Idee mit der Aussage aus a weiter zu arbeiten. Hatte nur Probleme dies Mathematisch tüchtig aufzuschreiben.

Aber eine Frage habe ich noch. Kann ich bei c, auch so ähnlich wie bei b Vorgehen also die Beziehung aus x² =x+1 verwenden oder wäre für c eine andere Vorgehensweise sinnvoller?

---

Für c) musst Du dann nur noch zeigen, dass $$x_{1,2} = \frac{1\pm\sqrt{5}}{2}$$Das hast Du ja schon in a) getan. Was aber dort nicht nötig gewesen wäre (siehe Bem2. in meiner Antwort).

Da mit b) bereits $L_n=x_1^n +x_2^n$ gezeigt wurde, reicht das aus. Ansonsten wäre es eine Wiederholung der identischen Rechnung.

---

Achso okay, wirklich nochmal vielen Dank, dann waren meine Gedanken, die ich nicht aussprechen wollte richtig. Da mir halt schon Aufgefallen ist das der Term ja der gleiche ist den ich ausgerechnet hatte in a. Ich glaube man sollte seinem Bauchgefühl einfach mal vertrauen.