Nullstellenproblem und Newton-Verfahren

Question

Hallo, folgende Ausgangslage:

Text erkannt:

In dieser Aufgabe soll iterativ die Stärke $d \in(0, R)$ einer Kugelschale mit Volumen $V>0$ und gegebenem Außenradius $R>0$ bestimmt werden, wobei angenommen werden kann, dass $V$ durch das Volumen einer Vollkugel mit Radius $R$ beschränkt ist, also
$V<\frac{4 \pi}{3} R^{3} .$

Ich soll nun eine Funktion f bestimmen, welche die Stärke d als Nullstelle besitzt und deren Auswertung ohne Wurzelberechnung auskommt. Zur Verdeutlichung der Stärke d hier eine Skizze: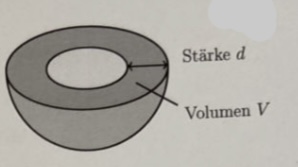

Text erkannt:

Stärke $d$ Volumen $V$

Das Ziel der Aufgabe soll sein, dass ich das Newton-Verfahren anwende, allerdings scheitert es gerade bei mir, so eine Funktion f zu finden. Kann mir hier bitte jemand weiterhelfen?

Answer 1

v = 4/3·pi·r³ - 4/3·pi·(r - d)³

oder

f(d) = v - 4/3·pi·r³ + 4/3·pi·(r - d)³ = 0

Damit würde man jetzt vermutlich das Newtonverfahren aufstellen.