Von wieviel Prozent der Wahlberechtigten ist Esther gewählt worden?

Question

Aufgabe:

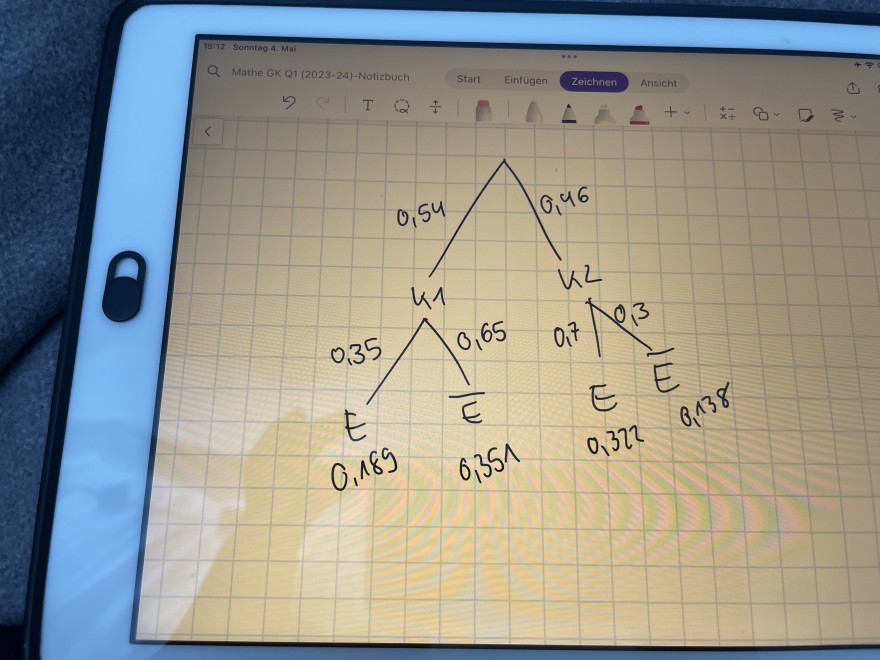
Bei der Wahl zum Kurssprecher für die belden Kurse K1 und K2 erhält Esther 35 % vom Kurs K1 und 70 % vom Kurs K2. 54 % der Wahlberechtigten sind aus Kurs K1, 46 % aus Kurs K2. Von wie viel Prozent der Wahlberechtigten ist Esther gewähit worden?

Problem/Ansatz:

Totale Warscheinlichkeiten Satz von Beyes

ich hab das Baumdiagramm gezeichnet aber mir fehlt der Ansatz für die Formel und das alles zu verstehen

Comments

Jetzt mußt Du das Ergebnis nur ablesen, wer hat alles Esther gewählt?

0.189+0.322=

---

Die Aufgabe hat nichts mit dem Satz von Bayes (mit A geschrieben) zu tun.

Dein Baumdiagramm stimmt. Wenn Du die Wahrscheinlichkeit für E wissen willst, dann addiere die Wahrscheinlichkeiten, die dort bei E stehen.

Answer 1

Satz der totalen Wahrscheinlichkeit

P(E) = P(K1 ∩ E) + P(K2 ∩ E)

P(E) = P(K1) * P(E | K1) + P(K2) * P(E | K2)

P(E) = 0.54·0.35 + 0.46·0.7 = 0.189 + 0.322 = 0.511