Aufgabe:
E=m*c^2 mathematisch ermitteln durch eine vorgegebene, beliebige, quadratische Funktion
Problem/Ansatz:
die beliebige mathematische, quadratische Funktion soll f(x)=x^2 sein
Differentiation f'(x)=(x^2)'=2x Umkehrfunktion fu=1/2x eingeschlossene Fläche: B=2,25
Integration F(x)=1/3*x^3 Umkehrfunktion Fu=(3x)^(1/3) eingeschlossene Fläche: A=1,5
Es gilt: A^2=B , daraus folgt E/m=c^2 E=Energie, m=Masse
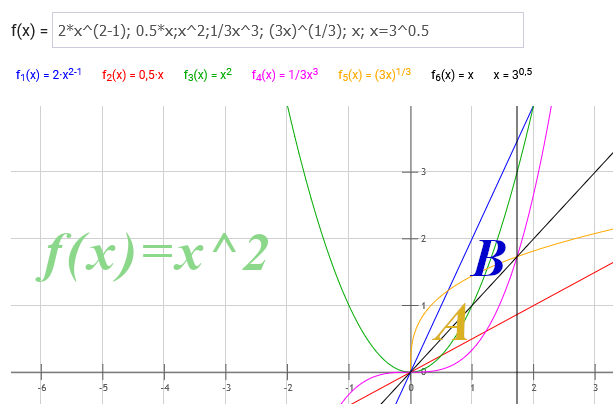
Text erkannt:
\( \begin{array}{l}f(x)=2^{*} x^{\wedge}(2-1) ; 0.5^{*} x ; x^{\wedge} 2 ; 1 / 3 x^{\wedge} 3 ;(3 x)^{\wedge}(1 / 3) ; x ; x=3^{\wedge} 0.5 \\ f_{1}(x)=2 \cdot x^{2-1} \quad f_{2}(x)=0,5 \cdot x \quad f_{3}(x)=x^{2} \quad f_{4}(x)=1 / 3 x^{3} \quad f_{5}(x)=(3 x)^{1 / 3} \quad f_{6}(x)=x \quad x=3^{0,5}\end{array} \)
eine zweimalige Differentiation des Integrales F(x) ergibt wiederum die Funktion f'(x) und diese hat die Fläche, mit Ihrer Umkehrfunktion f'u(x), der Größe B, daraus folgt: B/m=l, ein Leistungspotential l
Die Differentiation der Energie ergibt eine Leistung und deren Differentiation ergibt ein Leistungspotential dP/dt, physikalisch gesehen
.......dies müsste doch alles richtig sein, oder?
hatte die mathematische Gleichungen schon auf diesem Portal eingestellt, allerdings ohne Bezug zur Physik.......
Viele Grüße!