Nur mal zur Stetigkeit.
Diese Funktion ist in ganz R stetig.
Als Argument des ln kommen ja nur Zahlen ≥ 1 vor.
x^2+1 ist stetig und polfrei
ln für Argumente ≥ 1 auch
Die Zusammensetzung sollte daher stetig sein.
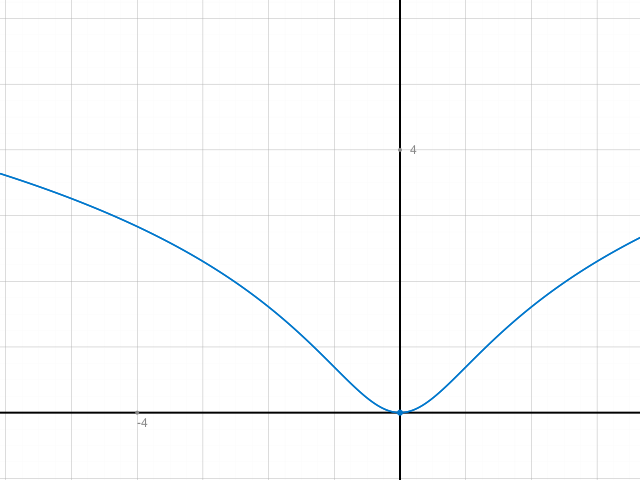
Im Graph sieht man gleich die einzige Nullstelle, die Symmetrie zur y-Achse.
Relative Extremalstellen sollte es ausser in (0/0) keine geben aber 2 Wendepunkte kannst du da wohl noch berechnen (symmetrisch zur y-Achse).