Wir haben seit ein paar Tagen das Thema Sinus, Cosinus, Tangens in Mathe. Jetzt soll ich eine Raute und ein Drachenviereck ausrechnen. Könnt ihr mir bitte mal bei der Aufgabe helfen.
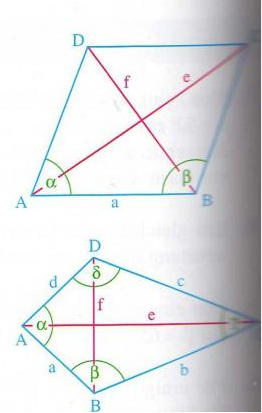
10. Bei einer Raute ABCD seien von den Stücken a, e, f, \( \alpha \) und \( \beta \) zwei Größen bekannt. Berechne die fehlenden Stücke.
a. \( a=17 \mathrm{cm} ; \alpha=69^{\circ} \)
b. \( a=34 \mathrm{cm} ; \mathrm{f}=61 \mathrm{cm} \quad \) e. \( \mathrm{e}=17,4 \mathrm{cm} ; \beta=126^{\circ} \)
c. \( \mathrm{e}=6,4 \mathrm{cm} ; \mathrm{f}=8,7 \mathrm{cm} \quad \) f. \( \mathrm{a}=8,3 \mathrm{cm} ; \mathrm{e}=11,8 \mathrm{cm} \)
d. \( \mathrm{f}=12,5 \mathrm{cm} ; \alpha=58^{\circ} \)
11. Von einem Drachenviereck ABCD seien die Seitenlängen \( a = 3,5 \mathrm{cm} \) und \( b = 6,5 \mathrm{cm} \), ferner die Winkelgröße \( \alpha = 88° \) bekannt.
Wie groß sind \( \mathrm{f}, \mathrm{e}, \beta, \gamma \) und \( \delta ? \)