Textaufgabe. Lineare Funktionen: In einem Öltank steht 4.8m hoch. Wann steht es in beiden Tanks gleich hoch?

Question

In einem Öltank steht das Öl 4,8m hoch. Das Öl wird über einen Schlauch in einen breiteren Tank umgefüllt, wobei der Ölspiegel im ersten Tank 5dm pro Stunde sinkt und im zweiten Tank um 4dm pro Stunde steigt.

Ermittle rechnerisch und grafisch, nach welcher Zeit das Öl in beiden Tanks gleich hoch steht.

Answer 1

Kleinerer Tank: f(x)=-5x+48

Größerer Tank: g(x)=4x

Schnittpunkt berechnen: f(x)=g(x)
-5x+48=4x   |+5x
48=9x   |/9
x=16/3

Nach 16/3 Stunden = 5 Stunden und 20 Minuten steht das Öl in beiden Tanks gleich hoch.

Grafisch: Du zeichnest beide Graphen und liest den Schnittpunkt ab:

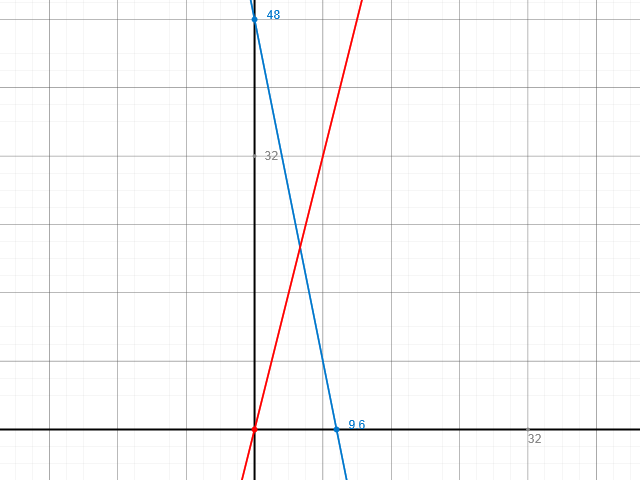
(Ich weiß leider nicht, wie man mit dem Tool den Schnittpunkt bestimmen kann, aber das kannst du sicher auch alleine, wenn du die Graphen zeichnest.)

Comments

Das Tool kann den Schnittpunkt noch nicht direkt ausgeben.

Daher rechnerisch x=16/3 h einsetzein in g oder f:

Kleinerer Tank: f(16/3) = -5*16/3 + 48 = 21,333 dm

Größerer Tank: g(16/3) = 4*16/3 = 21,333 dm