Lösen Sie die folgende Gleichung zeichnerisch (graphisch): -x² + 2x = 1

Question

Aufgabe: Lösen Sie die folgende Gleichung zeichnerisch (graphisch)

Ich habe zurzeit Parabeln in Mathe und habe mit dem zeichnen von Parabeln Probleme!

Die Aufgabe ist:

b) -x² + 2x = 1

Wie soll ich das genau lösen?

Answer 1

Wenn du einen Graphen zeichnen sollst, kannst du dir immer ein paar Werte ausrechnen und daraus den Graphen zeichnen. Da -x^2+2x ein Polynom zweiten Grades ist, kommt der Graph von -∞ und geht nach -∞.

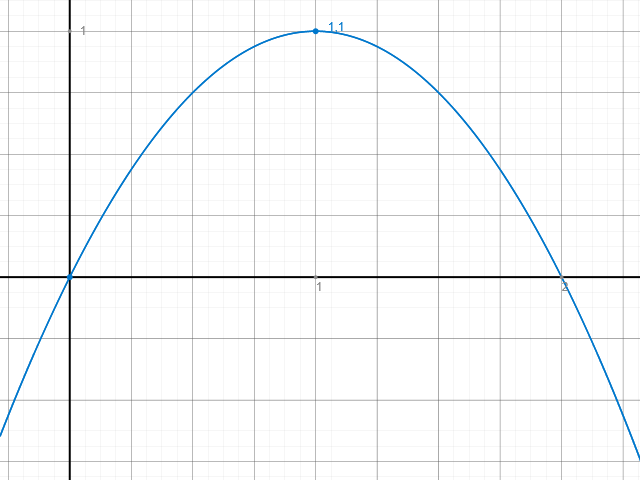
Nun überprüfst du, an welcher Stelle der Graph den Wert 1 hat: Das kannst du hier einfach ablesen, nämlich bei 1.

Also ist die Lösung der Gleichung -x²+2x=1: x=1

Comments

OKii das x=1  hab ich mithilfe der Formel ausgerechnet Xs = -b geteilt(bruchstrich) 2a und habe da 1 herausbekommen. Und das stimmt mit ihrer Lösung für x überein. Aber wie würde ich dann y herausfinden? Den bei ihrer Zeichnung ist ja der Scheitel auf S(1/1).

Answer 2

Vergleiche mal die Graphen von

linker Seite der Gleichung: y= -x^2 +2x = -x(x-2)        hat Nullstellen bei 0 und 2

rechter Seite der Gleichung: y=1

Normalparabel: y=x^2

Weil -x^2 die gleiche Öffnung hat, sind beide Parabeln deckungsgleich (kongruent).

Deshalb weiss man, dass die gesuchte Parabel den Scheitelpunkt in S(1/1) haben muss.

Man kann auch f(1) = -1^2 + 2*1 = -1 + 2 = 1 ausrechnen.

 

Schau dir eventuell mal hier die Videos zu Parabeln an:

https://www.matheretter.de/wiki/quadratische-funktionen