Hallo
Danke für die Angabe, die war sehr hilfreich. Deine Zeichnung oben ist leider nicht ganz vollständig gewesen. Das kleine Quadrat hätte auch noch schwarz sein müssen.
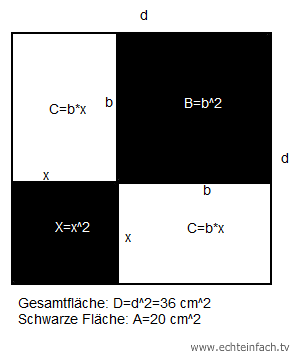
Skizze des Quadrats, Seiten und Flächen.
Hm. Ich wollte das allgemein lösen, das ist hier keine so gute Idee.
Also zum Ansatz:
Es gilt ja: A=X+B; (s. Skizze); A=x2+b2;
d=b+x; die Strecke d kann auch als Summe aus x und b geschrieben werden.
Umformen: b=d-x; Das wird eingesetzt.
x2+(d-x)2-A = 0;
x2+d2-2dx+x2-A = 0;
2x2-2dx+d2-A = 0; d=6, A=20,
2x2-12x+36-20 = 0; |*1/2
x2-6x+8 = 0; [1]
Der Satz von Vieta besagt nun Folgendes:
x2+px+q = 0; [2] //allgemeine quadratische Gleichung
für p und q gilt:
-p=x1+x2; x1und x2 sind die Lösungen der quadratischen Gleichung
q=x1*x2;
Der Vergleich von [1] und [2] ergibt dann:
p = -6; -> 6=x1+x2
q = 8; -> 8=x1*x2
Nun schaust Du genau hin und rätst quasi. In etwa so: 3+3 = 6, aber 3*3 = 9, kann es also nicht sein, 1+5=6 aber 1*5=5 ist es auch nicht, 2+4 = 6, 2*4=8 ist richtig ist also die Lösung.
Ich hoffe das hilft Dir weiter.
Die Aufgabe ist an sich nicht schwer, wenn man sofort den richtigen Ansatz wählt. Ansonsten kann es schon mal länger dauern.