Übertragen der Ziffern von Pi in ein lesbares Alphabet (A-Z). Wie vorgehen?

Question

Ich würde mir die Zahl Pi gerne in "Textform" anschauen.

Dazu müsste man die Ziffern in einem 26er-Zahlensystem darstellen (wobei 0-9 nicht enthalten sind, sondern nur A bis Z. Umlaute und ß vernachlässigen wir).

Wer hat eine Idee, wie man vorgehen müsste? Wie wandelt man 3,14159265359... am Sinnvollsten um?

Answer 1

Du stellst oft Fragen, die ich mir vor 15 Jahren auch stellte ... :-)  

Wenn 0..9 nicht enthalten sein sollen, nimmt man Basis 26 siehe http://www.gerdlamprecht.de/Kreiszahl.htm ganz unten

und per "Suchen + Ersetzen" 0 durch Q ... 9 durch Z ersetzen:

pi(26)=T.THIGBEBOHJHETDBXDGJWAKTGWJKYHNDUGRSARIPYLGGLWTCUBCKUNHEYGYOQBLKPLURCYZFGGNBAFBHDSVMZFROCWWEXZCCGYICIISYUAXLTKJSNJZFIRMXKVECGZQEIOWFEMKFOCBYVIVYYPHDP...

(berechne gerade 1 Mio Stellen weiter...)

Aber das hat einen Nachteil: Basis-Umrechnungen müssen von vorn alle Stellen linear durchgerechnet werden, d.h.

- schlecht parallelisierbar (Multitasking über mehrere Festplatten)

- enormer Speicherplatzverbrauch (pro Variable 13.3 Bio. Stellen!)

Außerdem findet man 12 stellige Ziffernfolgen erst so um die 8 Bio zu 80%.

(100% erst so bei 27.5 Bio. Stellen, ABER so viel sind noch nicht berechnet http://www.gerdlamprecht.de/BisZuWelcherNKalleStringKombi.htm)

Einfacher funktionieren Algorithmen, die aus 3 Ziffern 2 Buchstaben generieren (ungenutzte Bits auf den nächsten übertragen):

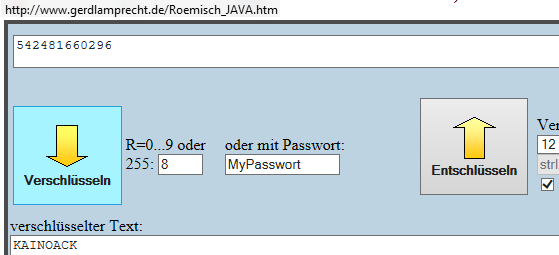
http://www.gerdlamprecht.de/Roemisch_JAVA.htm 2. Textkonverter Algorithmus 12 macht aus KAINOACK = 320269448074 bei Rotation R=0

bei R=1 -> 219158337963 -> und nach diesen Ziffernfolgen kann man leicht parallel suchen.

(habe Suche gerade gestartet...)

Ergebnis 1: habe Deinen Namen in Pi gefunden (relativ weit vorn diesmal): Position=29271477820

So, Algorithmus 2 ist mit 1 Mio. Dezimalstellen nach Basis26 Zeichensatz A...Z fertig:

normaler Code war: char(x+48) für Ziffern

pi(26)=3.3HIGBEBOHJHE3DB7DGJ6AK3G6JK8HND4G...

Diesmal Zeichensatz: 00=A  ... 26=Z. Code: char(x+65)

D.DRSQLOLYRTRODNLHNQTGKUDQGTUIRXNEQB...

NOAC in Basis 26 ohne Ziffern erst ab Basis26-Position=411220

NOACRBRLQZONOZSZGCDTCSOYVXQNSTGN...

Die ersten 20000 Stellen sind online:

Comments

Vielen Dank für die Informationen. Was kann man sich unter "Rotation R=0" und "R=1" vorstellen?

---

R=0 ist Normalfall.

Alles andere bedeutet Verschiebung des Zeichensatzes (Ergebnis sind Ziffern 0...9) siehe

https://de.wikipedia.org/wiki/Caesar-Verschl%C3%BCsselung  

Somit bekommt man 10 statt 1 mögliche "Suchstrings" -> und verzehnfacht somit die Wahrscheinlichkeit einen 12stelligen Ziffernstring zu finden.

---

So, habe jetzt 8 Mio. Stellen von Pi nach Basis 26 umgerechnet und über 48 verschiedene Zeichensätze eingebaut.

Schon das relativ kurze Wort Matriz wird erst nach über 380 Mio. durchsuchten Zeichen

an Basis26-Position=2912798 gefunden:

---

Und extra für Dich: http://www.lamprechts.de/gerd/php/suche-wort-in-pi-Algo12_29Mrd.php

Basis30-Position=985214 (Dezi-Nachkommastelle:29271477820)
Nachkommastellen=KAINOACKTVHZÄSLYDGEÜCZSFSXWTQPQLOWCAZLZEDYVÜQGHNHE...

Answer 2

Wie kommt man auf so eine Idee? ;-)

Du könntest \(\pi\) vom Dezimalsystem in das Zahlensystem zur Basis 26 umrechnen (bzw. könnte man das ein Computerprogramm machen lassen; ich glaube, dass will niemand per Hand rechnen).

Comments

Zur Idee: Da Pi unendlich viele, nicht-periodische Nachstellen hat, ist es wahrscheinlich, dass jede erdenkbare Zahlenkombination in ihr enthalten ist, also auch jedes erdenkliche Wort (sofern übertragen) und jeder erdenkliche Satz etc. Darüber finden sich im Netz und auch hier auf Mathelounge.de einige Diskussionen. Da wäre es doch mal interessant, die Buchstaben der ersten Stellen vor Augen zu haben!

Gut, aber wie würdest du beim Übertrag vom 10er System ins 26er System vorgehen?

Schließlich hätte man mehrere Möglichkeiten, wenn man kein Umwandlungssystem/keinen Codieralgorithmus definiert. Z. B. 3,1415926 als:

14 15 9 26 oder 1 4 1 5 9 2 6 oder ...

---

Ich dachte eigentlich an folgendes: Für jede Zahl \(x\in\mathbb{N}\) gibt es ein eindeutiges \(n\in\mathbb{N}\) und eindeutige \(a_i\in\{0,...,25\}, 1\leq i\leq n,\) sodass \(x=\sum\limits_{i=0}^{n} a_i\cdot 26^i\).

Z.B. ist \(1773=2\cdot 26^2+16\cdot 26^1+5\cdot 26^0.\) Das würde man im Stellenwertsystem zur Basis 26 dann meist so schreiben: \(1773_{10}=2G5_{26}\) (man benutzt dann A für 10, B für 11, ..., P für 25).
Du willst keine Zahlen, sondern nur Buchstaben haben, also könntest du 0 durch A ersetzen, 1 durch B, 2 durch C, ..., P durch Z (oder irgendwie anders).

---

Du hast Recht, statt eines Zahlensystems könnte man sich auch einen Algorithmus basteln, der Ziffern direkt überträgt zu Buchstaben.