Wie groß ist die Fläche, die der Graph von f mit der x-Achse einschließt? (Flächenberechnung, Vektoren und Integrale)

Question

Aufgabe Prüfungsvorbereitung:

Gegeben ist die Funktion \( f \) mit \( f(x)=0,5 x^{2}\left(x^{2}-4\right) \).

a) Wie groß ist die Fläche, die der Graph von \( f \) mit der \( x \)-Achse einschließt?

b) Der Graph von \( f \) und die Gerade mit der Gleichung \( y=-2 \) begrenzen eine Fläche. Berechnen Sie deren Inhalt.

c) Untersuchen Sie, wie sich der Flächeninhalt \( \mathrm{A} \) aus Teilaufgabe a) verändert, wenn statt der Funktion \( f \) die Funktion \( g \) mit \( g(x)=k \cdot f(x) \) mit \( k>0 \) gegeben ist.

Answer 1

Hi,

a) Berechne die Nullstellen von f(x). Das sind die Intervallgrenzen für dein(e) Integral(e)

b) Differenzenfunktion h(x) = f(x) - (-2). Nullstellen von h(x) bestimmen. Integral von h(x) über den Intervallgrenzen (also zwischen den Nullstellen) bestimmen.

c) Nullstellen ändern sich nicht. Einfach wieder integrieren oder aber argumentieren, dass sich der k-fache Flächeninhalt ergibt.

Tipp 1: Eine Skizze der Funktion kann wahre Wunder bei der Ansatzsuche bewirken.

Tipp 2: Mathe LK und Probleme mit solchen Standardaufgaben -> Nachhilfe suchen (am besten andere Mitschüler, die gut erklären können).

Tipp 3: Vektoren kommen gar nicht vor.

Gruß

Answer 2

Aufgabe 11

a) Hier siehst du den Graphen der Funktion:

Du berechnest die Nullstellen und nimmst diese als untere und obere Grenze.

b) Hier berechnest du die Extremstellen der Funktion. Die beiden äußeren bilden wieder deine Grenze.

c) Du berechnest die Aufgabe a) erneut, aber jetzt mit der Funktion 0.5kx²(x²-4). Und untersuchst, wie dich dieses Ergebnis von a) für k>0 unterscheidet. Wird es größer, kleiner, etc.

Soviel zur Aufgabe 11. Bei Fragen einfach melden ;)

Gruß
EmNero

Answer 3

f ( x ) = 0.5 * x^2 * ( x^2 - 4 )

Schnittpunkt mit der x-Achse

0.5 * x^2 * ( x^2 - 4 ) = 0
Ein Produkt ist dann 0 wenn mindestens einer der Faktoren 0 ist
x^2 = 0
x = 0
und
x^2 - 4 = 0
x^2 = 4
x = +2
x = -2

Nullstellen -2, 0 , +2

Die Funktion ist achsensysmmetrisch zu y-Achse
deshalb brauchen wir nur eine Seite berechnen
Stammfunktion
∫ 0.5 * x^2 * ( x^2 - 4 ) dx
∫ 0.5 * x^4  - 0.5 * x^2 * 4  dx
∫ 0.5 * x^4  - 2 * x^2 dx
0.5 * x^5 / 5 - 2 * x^3 / 3

[ 0.5 * x^5 / 5 - 2 * x^3 / 3 ]₀²
0.5 * 2^5 / 5 - 2 * 2^3 / 3 - ( 0.5 * 0^5 / 5 - 2 * 0^3 / 3)
3.2 - 5.33333
-2.13333
Als Fläche posiziv
2.13333
Gesamtfläche
2.13333 * 2 = 4.26666

b.)

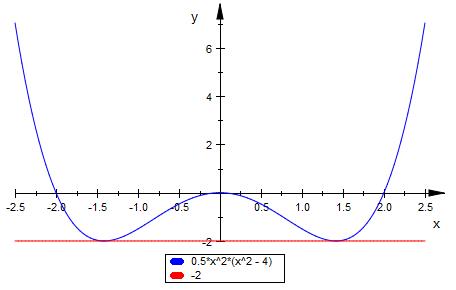
Schnittpunkt der blauen und roten Funktion
f ( x ) = -2
0.5 * x^2 * ( x^2 - 4 ) = -2
x^2 * ( x^2 - 4 ) = -4
z  = x^2
z * ( z - 4 ) = -4
z^2 - 4z = -4  | quadr.Ergänzung oder pq-Formel
z^2 - 4z + 2^2 = -4 + 4
( z - 2 )^2 = 0
z - 2 = 0
z = 2
z = x^2 = 2
x = ± √ 2
x = ± 1.414

Wir betrachten nur die rechte Seite. Gesucht ist die Fläche
Rechteck ( 2 * 1.414 ) - ∫ f ( x ) dx zwischen 0 bis +1.414
A = 2.828 - [ 0.5 * x^5 / 5 - 2 * x^3 / 3 ]₀^1.414
A = 2.828 - 1.32
A = 1.508
Gesamtfläche mal 2
1.508 * 2
3.017

c.)
g (x ) = k * f ( x )
Die Nullstellen bleiben erhalten.

Stammfunktion von g ( x )
k * [ 0.5 * x^5 / 5 - 2 * x^3 / 3 ]

Entspricht der Multiplikation der Fläche aus a.)
mit k