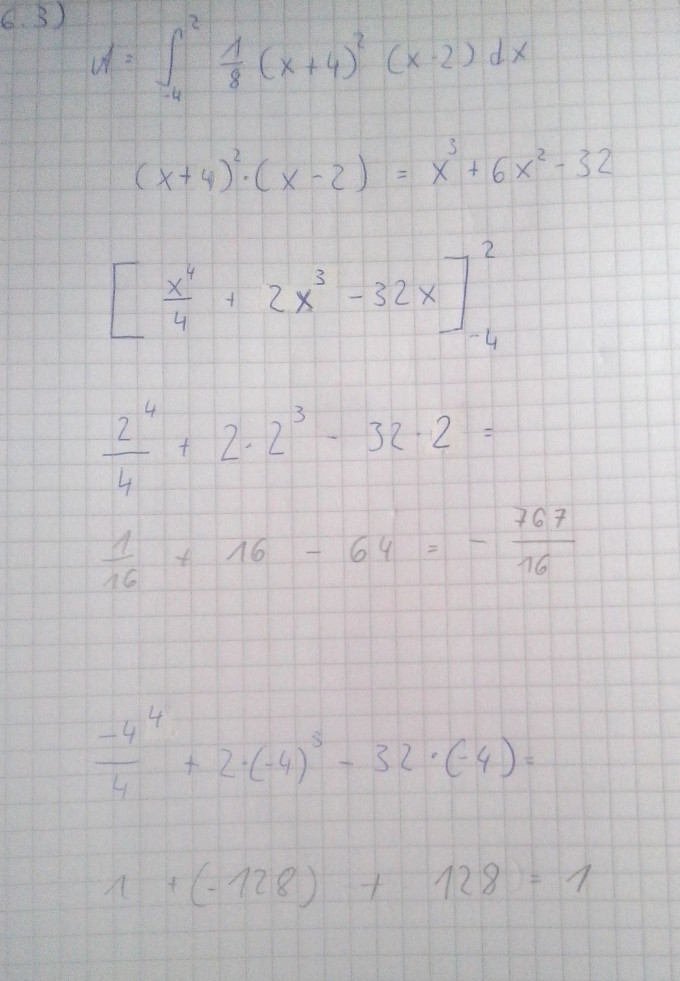Aufgabe:
6.0 Gegeben ist die reelle Funktion \( \mathrm{f} \) durch die Gleichung
\( f(x)=\frac{1}{8}(x+4)^{2}(x-2) \quad \text { mit } \quad D_{f}=R \)
Der Graph der Funktion \( f \) heißt \( G_{f} \).
6.1 Zeigen Sie rechnerisch, dass die Funktion F mit der Gleichung \( \mathrm{F}(\mathrm{x})=\frac{1}{32} \mathrm{x}^{4}+\frac{1}{4} \mathrm{x}^{3}-4 \mathrm{x}+2 \) eine Stammfunktion der Funktion f ist. Ihr Graph wird mit \( \mathrm{G}_{\mathrm{F}} \) bezeichnet.
6.2 Ermitteln Sie die Stammfunktion \( \mathrm{F}_{\mathrm{c}} \) von \( \mathrm{f} \), die durch den Tiefpunkt T des Graphen \( \mathrm{G}_{\mathrm{f}} \) verläuft. Treffen Sie eine Aussage zur Lage des Graphen von \( F_{e} \) bezüglich des Graphen \( \mathrm{G}_{\mathrm{F}} \) im Koordinatensystem.
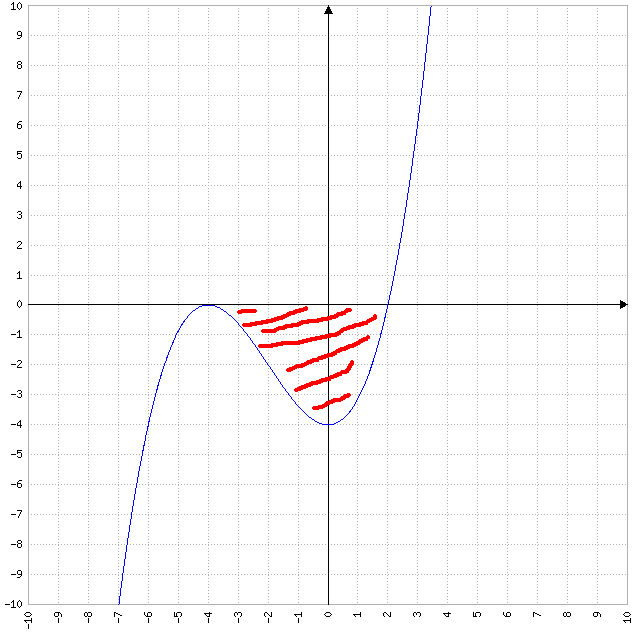
6.3 Der Graph \( \mathrm{G}_{f} \) schließt mit der Abszissenachse eine Fläche vollständig ein.
Ermitteln Sie den Inhalt dieser Fläche.
Skizze:
Mein Lösungsweg: