Rekursive Folge. Berechnen Sie den Grenzwert n→∞ für a_(n+1) = 1/2 (a_(n) + P/a_(n)) ; a1 = 1.

Question

Gesucht wird der Grenzwert der rekursiven Folge:

\( a_{n+1}=\frac{1}{2}\left(a_{n}+\frac{P}{a_{n}}\right) ; \begin{array}{l}a_{1}=1 \\ p \in \mathbb{R}\end{array} \)

Comments

Tipp: Setze für a_n+1 und für a_n einfach mal a ein und löse die (quadratische) Gleichung nach a auf.

Das wäre(n) alle möglichen Grenzwerte. Du weisst aber noch nicht, ob sie es wirklich sind.

Vermutlich dann verschiedene Möglichkeiten für P unterscheiden. 

EDIT: Beachte ähnliche Aufgaben. Bsp: https://www.mathelounge.de/138349/grenzwert-rekursive-folge-a-1-1-a-n-1-2·a-n-1-4·a-n

---

Also: a = 1/2(a + p/a) und nach a umgestellt liefert a =p.

heißt das mein Grenzwert ist p wenn ich an gegen ∞ laufen lasse?

Answer 1

Profis erkennen sofort den Iterationsalgorithmus für die Wurzel. Lu & Mathechoach haben die Umstellung gezeigt.

Zur Überprüfung der theoretischen Berechnung eignet sich der Iterationsrechner:  

http://www.gerdlamprecht.de/Roemisch_JAVA.htm##@N@B0]=1;b=25;a=1;//Abbruch%20a%3C1e-15@N@Bi+1]=(@Bi]+b/@Bi])/2;a=@A@Bi+1]-@Bi]);@Ni%3E8@N0@N0@N#

(LINK endet mit N# und beinhaltet den kompletten Code)  siehe Bild:  

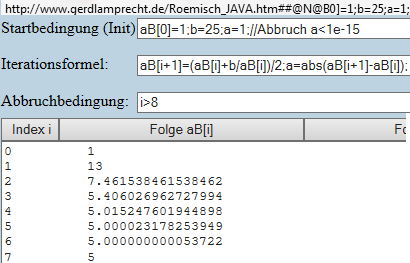
ABER bei negativem Startwert (b < 0) gibt es keine Konvergenz! 

b=-3 -> Bi-stabiler Generator, der zwischen 1 und -1 hin & herspringt

andere negative Startwerte:  Pseudo-Zufallsgenerator (wilde Sprünge)

Wenn man nur positive Werte für b eingibt, kann man die elegantere Abbruchbedingung  

a<1e-15 angeben, denn dann ist die maximale Genauigkeit für kleine Zahlen erreicht. Bei größeren Zahlenwerten muss auch die Abbruchbedingung vergrößert werden -> für viele zu kompliziert, deshalb universell i>8 denn das funktioniert immer...

Answer 2

 a = 1/2(a + p/a) |  nach a umstellen gibt nicht a=p

2a = a + p/a

a = p/a

a^2 = p

a = √p

p darf also nicht kleiner als 0 sein, wenn ein reeller Wert rauskommen soll.

Aber, ob für a₁=1 zwingend zu diesem Grenzwert kommst, musst du zusätzlich noch anderswie  zeigen. Such mal die entsprechenden Sätze im Skript. 

Answer 3

a_n+1 = 1/2·(a_n + p/a_n)

Wenn es einen Grenzwert gibt dann ändert sich a_n+1 gegenüber a_n nur noch unwesentlich. Sodass für den Grenzfall a_n+1 = a_n gilt

Man setzt dann allgemein a = a_n = a_n+1 und löst nach a auf.

a = 1/2·(a + p/a)

2·a = a + p/a

a = p/a

a^2 = p

a = ±√p

Du solltest jetzt nochmal prüfen was z.b. für negative werte von p passiert. Weiterhin mussten wir noch die Konvergenz nachweisen. Z.b. Das sich der errechnete Wert immer Dichter an der Wurzel von p befindet als der Startwert.