$$ f(x)= \frac{100}{1+19e^{-0,2x} } $$
ich weiß nicht wie ich diesen term ableite...
im intermet steht nach der Quotienten und Kettenregel aber ich sehe hier nur die kettenregel, da nur der nenner ein x enthält und die Ableitung von 100 eh null wäre
kann mir jemand helfen und zeigen wie ich den term nun ableiten muss
und wie kommt man von:
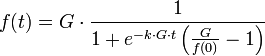
auf:
$$ f'(t) = k \cdot f(t) \cdot (G - f(t)) $$
das muss doch durch einfaches ableiten möglich sein ...
Gruß