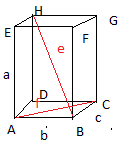
Ich soll Beweisen das e^f senkrecht zueinander stehen.
Mein bisheriger Weg.
e*f=0 > rechter Winkel = senkrecht
e=-c-a+b
f=b+c
=> e*f=(-c-a+b)*(b+c)
=-b*c-c^2-a*b-a*c+b^2+b*c
[-b*c=0 , -a*b=0 , a*c=0 , b*c=0] da Skalarprodunkt 0 ist
es bleibt also -c^2 und b^2 übrig.. bloß was bedeutet dies nun? Oder habe ich bisher was falsch gemacht?