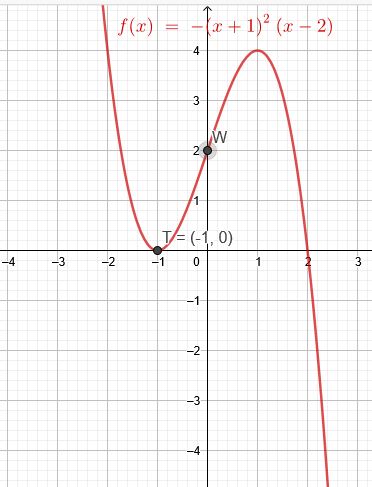
Bestimme die Funktionsgleichung einer ganzrationalen Funktion dritten Grades, mit gegebenen Wende- und Tiefpunkt.

Question

Hallo

Aufgabe 1: Bestimme die Funktionsgleichung einer ganzrationalen Funktion dritten Grades deren Graph im Punkt W (0 | 2) einen Wendepunkt und im Punkt T (-1 | 0) einen Tiefpunkt besitzt.

Aufgabe 2: Bestimme die Funktionsgleichung einer ganzrationalen Funktion vierten Grades, deren Graph symmetrisch zur y-Achse ist durch A (0 | -1), B(1 | 1) und C ( 2|-5) verläuft.

Answer 1

Bestimme die Funktionsgleichung einer ganzrationalen Funktion dritten Grades deren Graph im Punkt W (0 | 2) einen Wendepunkt und im Punkt T (-1 | 0) einen Tiefpunkt besitzt.

Linearfaktorenform:

f(x)=a(x+1)^2(x-N)

im Punkt W (0 | 2) einen Wendepunkt:

f(0)=a(0+1)^2(0-N)=-aN=2

\( a=-\frac{2}{N} \)

\(f(x)=-\frac{2}{N}(x+1)^2(x-N)=-\frac{2}{N}(x^2+2x+1)(x-N)\\=-\frac{2}{N}(x^3-Nx^2+2x^2-2Nx+x-N)\)

\(f'(x)=-\frac{2}{N}(3x^2-2Nx+4x-2N+1)\)

\(f''(x)=-\frac{2}{N}(6x-2N+4)\)

\(f'(0)=-\frac{2}{N}(-2N+4)=0\)

N=2

\( a=-1\)

f(x)=-(x+1)^2(x-2)

Answer 2

Aufgabe 1: Bestimme die Funktionsgleichung einer ganzrationalen Funktion dritten Grades deren Graph im Punkt W (0 | 2) einen Wendepunkt und im Punkt T (-1 | 0) einen Tiefpunkt besitzt.

f(0) = 2

f''(0) = 0

f(-1) = 0

f'(-1) = 0

Dann gehe auf die Seite http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm und lass dort die Gleichungen aufstellen und das lösen. Dann probierst du es schriftlich nachzuvollziehen

Comments

Aufgabe 2: Bestimme die Funktionsgleichung einer ganzrationalen Funktion vierten Grades, deren Graph symmetrisch zur y-Achse ist durch A (0 | -1), B(1 | 1) und C ( 2|-5) verläuft.

f'(0) = 0

f'''(0) = 0

f(0) = -1

f(1) = 1

f(2) = -5

Auch hier lässt du die Funktion erstmal bei http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm berechnen, bevor du dich selber daran setzt es selber handschriftlich zu rechnen.

---

Aufgabe 2
Funktioniert glaube ich nicht.
Der Steckbriefrechner ermittelt aus den 3 Punkten eine
Funktion 2.Grades.

Hier muß doch zu Fuß ( Symmetrie zur y-Achse )
f ( x ) = a*x^4 + b*x^2 + c
berechnet werden.

---

Gib mal meine Bedingungen in den Steckbriefrechner über cut und paste ein.

---

Wie kommst du auf

f'(0) = 0

f'''(0) = 0

---

Achsensymmetrie bedeutet der Faktor vor dem x ist null und der Faktor vor dem x^3 ist null. Das erreicht man mit den beiden Bedingungen.

---

Wegen der Achsensymmetrie ist f ´( 0 ) = 0
Das fiel mir nachher auch ein.

f ´´´ ( 0 ) = 0  könnte ich mir so nicht herleiten.

Gut. Meine Fragen sind beantwortet.

Answer 3

1) f(x) = a x³ + b x² + c x + d

f(0) = 2

f '' (0) = 0

f(-1) = 0

f ' (-1) = 0

einsetzen -> a,b,c,d

2)

f(x) = a x⁴ + b x² + c  [Symmetrie]

Punkte einsetzen:

f(0) = -1  .....

-> a,b,c