Funktion dritten Grades, deren Graph in W (0 | 3) und in T (1 | 1) einen Tiefpunkt hat?

Question

Wie erstelle ich eine Gleichung aus diesen Informationen?

Bestimmen Sie die Gleichung einer ganzrationalen Funktion dritten Grades,

deren Graph in W (0 | 3) und in T (1 | 1) einen Tiefpunkt hat

Answer 1

Bestimmen Sie die Gleichung einer ganzrationalen Funktion dritten
Grades, deren Graph in W (0 | 3) und in T (1 | 1) einen Tiefpunkt hat

f ( x ) = a*x³ + b*x² + c*x + d
f ´( x ) = 3 * a * x² + b* x + c
f ´´ ( x ) = 6 * a * x + b

f ( 0 ) = 3 
f ´´ ( 0 ) = 0  | Krümmung am Wendepunkt = 0
f ( 1 ) = 1
f ´ (1 ) = 0  | Steigung am Tiefpunkt = 0

4 Aussagen für 4 Unbekannte.
Kannst du das allein ?

Ansonsten wieder melden.

Zur Kontrolle
f(x) = x³ - 3·x + 3

Comments

Von einem Wedepunkt ist nicht explizit die Rede. Die Aufgabe ist  missverständlich.

---

doch doch, es hat dort einen wendepunkt, habs nur vergessen zu schreiben :)

---

@ georgborn eine frage wie kommst du auf f ´´ ( 0 ) = 0 ?

---

f(0) = 3      -->     d                      = 3

f´´(0) = 0   -->     6ax + 2b         = 0  -> ich weiß nicht was ich damit anfangen soll ....

f(1) = 1      -->     a + b  + c + 3  = 1

f´(1) = 0     -->     a + b + c         = 1

mach ich das richtig oder bin ich gerade total auf dem falschen gleis?

---

beim letzten = 0

---

@ georgborn eine frage wie kommst du auf f ´´ ( 0 ) = 0 ?
Richtig. Dies ist in der Aufgabenstellung nicht angegeben.
Ohne diese Angabe ist aber die Aufgabe nicht zu lösen.

---

ok, wie mache ich denn jetzt weiter georgborn?

---

Dann überprüfe ich einmal

f ( x ) = a*x³ + b*x² + c*x + d
f ´( x ) = 3 * a * x² + b* x + c
f ´´ ( x ) = 6 * a * x + b

f ( 0 ) = 3 
f ´´ ( 0 ) = 0  | Krümmung am Wendepunkt = 0
f ( 1 ) = 1
f ´ (1 ) = 0  | Steigung am Tiefpunkt = 0

f ( 0 ) =  a*0³ + b*0² + c*0 + d = 3  => d = 3
f  ´´ ( 0 ) =  6 * a * 0 + b = 0  => b = 0

f ( x ) = a*x³ + c*x + 3
f ´( x ) = 3 * a * x² + c

f ( 1 )  = a*1³ + c*1 + 3 = 1
f ´ ( 1 ) = 3 * a * 1² + c = 0

a  + c + 3 = 1

3 * a + c = 0
c = -3a

a  + c + 3 = 1
a -3a  = -2
-2a = -2
a = 1

c = -3a
c = -3*1
c = -3

f(x) = x³ - 3·x + 3

---

ganz oben 2. Ableitung: 6 * a * x + 2 * b

---

Richtig. Dort ist ein Fehler.
Da b aber relativ früh rausfliegt
f  ´´ ( 0 ) =  6 * a * 0 + 2 * b = 0  => b = 0

Hat der Fehler keinen Einfluß auf das Ergebnis.

---

alles klar, dann habe ich das jetzt verstanden, danke schön :)

---

Gern geschehen. Dazu ist das Forum ja da.

---

a  + c + 3 = 1

3 * a + c = 0
c = -3a

hi kannst du das bitte erklären wie du auf mal 3 kommst

---

Die berechnete Funktion stimmt.
Von einem Wendepunkt habe nicht gesprochen.
Hast du deine Frage zwischenzeitlich
geändert ?

---

siehe oben
2 Aussagen sind übrig
a + c + 3 = 1
3 * a + c = 0

Die nächtse Zeile ergibt sich aus der 2.Aussage
c = -3a

Answer 2

f(x) = ax^3+bx^2+cx+d

f(0) = 3

f '(0) = 0

f(1) = 1

f' '(1) = 0

Comments

Du hast Wendepunkt und Tiefpunkt vertauscht.

f ´´( 0 ) = 0
f ´( 1 ) = 0

Answer 3

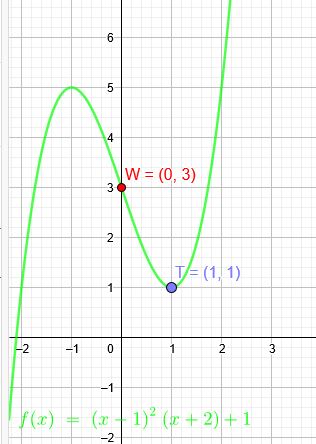
Gleichung einer ganzrationalen Funktion dritten Grades, deren Graph in $W (0 | 3)$ einen Wendepunkt und in $T (1 | \red{1})$ einen Tiefpunkt hat.

Ich verschiebe den Graphen um $\red{1}$Einheit nach unten: $T (1 | \red{1})$ → $T ´(1 | 0)$

$f(x)=a\cdot(x-1)^2\cdot(x-N)$

$W (0 | 3)$  →   $W´ (0 | 2)$:

$f(0)=a\cdot(0-1)^2\cdot(0-N)$ →  $f(0)=a\cdot(-N))$

$a\cdot(-N)=2$   →$a=-\frac{2}{N}$

$f(x)=-\frac{2}{N}\cdot[(x-1)^2\cdot(x-N)]=-\frac{3}{N}\cdot(x^3-Nx^2-2x^2+2xN+x-N)$

$f´(x)=-\frac{2}{N}\cdot(3x^2-2Nx-4x+2N+1)$

$f´´(x)=-\frac{2}{N}\cdot(6x-2N-4)$

Wendepunkteigenschaft:

$W´ (0 | ...)$:

$f´´(0)=-\frac{2}{N}\cdot(-2N-4)$

$-\frac{2}{N}\cdot(-2N-4)=0$       $N=-2$      $a=\frac{-2}{-2}=1$

$f(x)=(x-1)^2\cdot(x+2)$

um $\red{1}$Einheit nach oben:

$p(x)=(x-1)^2\cdot(x+2)+1$