Beweise 1+ln(x)<=x gilt für x > 0

Question

ich soll beweisen das gilt: 1+ln(x) <= x gilt für x > 0 mit 1+y <= exp(y) für y∈R

Da muss man ja irgendwie von 1+ln(x) <= x auf 1+x <= exp(x) kommen.

Da komme ich aber beim besten Willen nicht drauf, da wenn ich auf die 1 exp() werfe ja e^1 draus wird.

Oder muss man bei dieser Rechnung irgendwo abschätzen?



 

 

Comments

Zum Zusammenhang von Logarithmus und Exponentialfunktion gibt es hier: https://www.matheretter.de/wiki/logarithmus Material und ein Gratisvideo. Vielleicht hilft  dir das bereits bei deiner Frage. (?)

---

Nicht wirklich...

1+ln(x) <= x | exp()
exp(1+ln(x)) <= exp(x)

exp(1) * x <= exp(x)

Und nun? Wie komme ich hier weiter?

Es sieht ja fast schon so aus wie 1+y <= exp(y)

nur das e * x >= 1+x ist für x >= 1 aber kleiner für x<1

Soll man da was abschätzen?

Answer 1

Alternativ vielleicht auch so ganz schön:

 

1+ln(x)≤x als

f(x)=x-1-ln(x) interpretieren.

 

Für x>0 einziges Minimum bei f'(x)=(x-1)/x -> x=1

Das Minimum nimmt dabei den Wert f(1)=0 an.

 

Folglich sind alle Werte f(x)=x-1-ln(x)≥0.

Das nur noch wieder umstellen: x≥1+ln(x)

 

Grüße

Answer 2

 1+y <= exp(y) ist wohl die Voraussetzung, die du aus dem Kurs kennst.

Skizze rot-blau für 1+x und e^x

Violett-grün: eure Behauptung

Türkis-orange(?): Umkehrfunktionen von rot und blau: 

Graphen von lnx und x-1

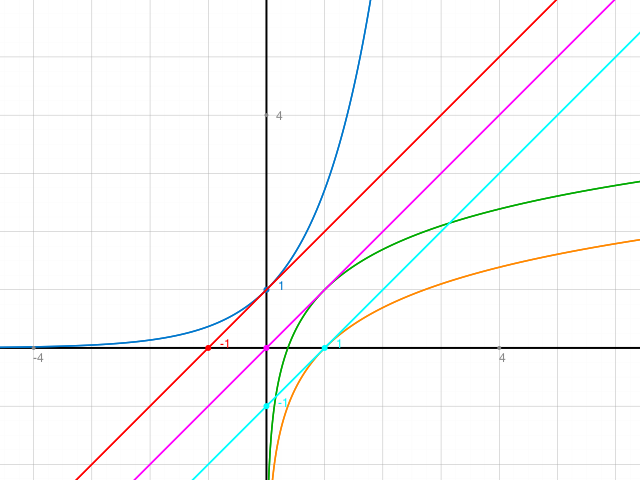
Witz von Umkehrfunktionen: entweder man spiegelt an x=y oder man zeichnet das sie auf ein durchsichtiges Papier und kippt die Figur, bis man der lnx aussieht wie e^y . Beim Kippen hat man den Vorteil, dass man die Achsen nicht umbenennen muss.

Wenn du y₁ = ln(x₁) hast, ist nach Definition x₁ = e^y₁ und das für alle x₁ > 0.

Deshalb kannst du in deiner Voraussetzung y ersetzen durch ln(x) und e^y durch x

Deine Voraussetzung y+1 ≤ e^y wird so direkt zu 

 ln(x) + 1 ≤ x         qed.

Comments

Aha, also was du gemacht hast ist dann einfach:

1 + ln(x) <= x | exp()
exp(1) + x <= exp(x)
e + x <= exp(x)
da e > 1
1 + x <= exp(x)

?

---

Nein mit der 1 mache ich gar nichts.

Ich ersetze lnx durch y und dafür e^y durch x. fertig. Ich muss da nichts umformen.

Das klappt nur, wenn ich den Graph wie beschrieben kippe.