Summenzeichnen umformen, vollständige induktion.

Question

Halo alle mal!
Ganz direkt, kann jemand mir zeigen der Rechnerweg von: Wird:


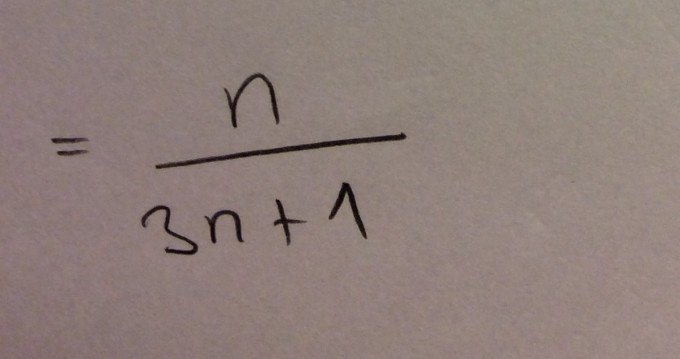
Das ist ein kleine Teil von volständige induktion Aufgabe, ich komm mir nicht weiter wie man die summezeichnen umformen bzw. weg machen. Ist das was mit ∑ⁿ_{i=1   = n(n+1)/2 zu tun?}   Danke schonmal,

Comments

Willst du jetzt den Induktionsschritt sehen oder wie man das direkt per Teleskopsumme berechnen kann?

---

direkt berechnen wie man das summenzeichnen weg machen kann.. dankeee ^^

Answer 1

$$\sum_{i=1}^n \frac{1}{(3i-2)(3i+1)} = \sum_{i=1}^n \frac{1}{3} \left( \frac{1}{3i-2} - \frac{1}{3i+1} \right) \\ = \frac{1}{3} \cdot \left( \sum_{i=1}^n \frac{1}{3i-2} - \sum_{i=1}^n \frac{1}{3i+1} \right) \\ = \frac{1}{3} \cdot \left( \sum_{i=0}^{n-1} \frac{1}{3i+1} - \sum_{i=1}^n \frac{1}{3i+1} \right) = \frac{1}{3} \cdot \frac{3n}{3n+1} = \frac{n}{3n+1}$$

Gruß

Answer 2

Hi,
es gilt $$\frac{1}{(3i-2)(3i+1)} = \frac{1}{3} \left( \frac{1}{3i-2} - \frac{1}{3i+1} \right)$$
$$\sum_{i=1}^N \frac{1}{(3i-2)(3i+1)} = \frac{1}{3} \sum_{i=1}^N \left( \frac{1}{3i-2} - \frac{1}{3i+1} \right) = \frac{1}{3} \left( 1 +\sum_{i=2}^N \frac{1}{3i-2} - \sum_{i=1}^{N-1} \frac{1}{3i+1} - \frac{1}{3N+1} \right) = \frac{1}{3} \left( 1 + \sum_{i=1}^{N-1} \frac{1}{3i+1} - \sum_{i=1}^{N-1} \frac{1}{3i+1} - \frac{1}{3N+1} \right) = \frac{N}{3N+1}$$