Hallo ihr Experten,
vielleicht könnt ihr mir bei dieser Extremwertaufgabe helfen:
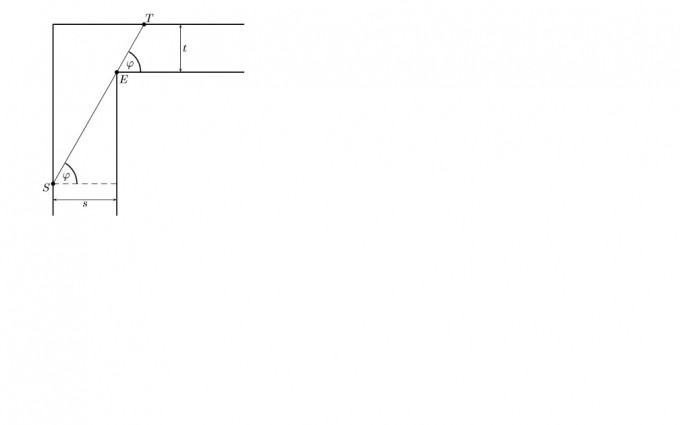
Es soll ein Balken um die Ecke transportiert werden, wobei die Dicke nicht berücksichtigt werden muss. Wie lang darf der Balken maximal sein, damit er durchpasst? Die maximale Länge soll als L bezeichnet werden.
Es ist gegeben: f(φ) = [ST] φ ∈ [0; π/2]
Nun habe ich folgende Fragen:
1. Wie hängen f(φ) und L miteinander zusammen? Kann man da eine Gleichung aufstellen?
2. Wenn s = 3m und t = 6m , wie berechne ich L? Muss ich einen Wert für den Winkel ausrechnen?
Ich habe ewig lange herumprobiert und gegoogelt, aber ich habe keinen vernünftigen Ansatz. Da mir die Grundidee für die Aufgabe fehlt (und wahrscheinlich auch das Grundwissen), wäre ein ausführlicher Lösungsansatz sehr nett, der gerne auch mal die Basics erklärt. Den Satz des Pythagoras etc. kenne ich zwar, ich habe aber ein Problem damit, das Wissen auf die Aufgabe anzuwenden.
Ich würde mich sehr über eine Antwort freuen.
Ein Studiums-Neuling