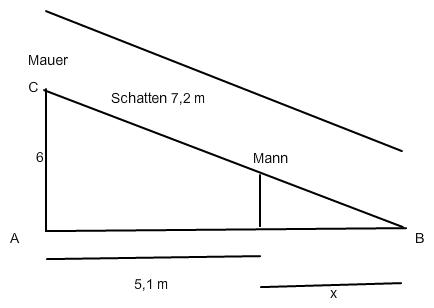
Textaufgabe: Eine 6m Hohe Mauer wirft einen 7,2 m langen Schatten. Wie groß ist ein Mann, der sich gerade noch ganz im Schatten befindet, wenn er 5,1 m vor der Mauer steht ?
Lös: 1,75 m
Ich habe folgende Skizze gemacht, weiss aber nicht, ob sie so stimmt.
Meine Lösung, die nicht stimmt. Wüsste gerne, was an dem Pythagoras falsch ist.
AB^2 = BC^2 - AC^2
AB^2 = 7,2^2 - 6^2 =15,84 --> AB=3,98 Hier wäre also die Gesamtlänge AB kürzer als die Strecke von Mann zu Mauer ????? FALSCH, aber warum.
-----
Dann habe ich noch das Ganze von hinten aufgerollt unter Verwendung der Mann-Größe m=1,75 m.
Strahlensatz :AC : m = (5,1 m + x) : x
600 cm : 175 cm = (510 cm + x) : x
600x = 175 * (510 + x)
600x = 89250 + 175x
425x = 89250
x = 210 (cm)
Überlegung: 510 + 210 = 720 = AB = genauso lang, wie die schiefe Strecke BC (wäre kein Dreieck)
Wer weiss Rat ?
LG
Uli