Glücksrad hat drei gleich große 120°-Sektoren

Question

,,

Ein Glücksrad hat drei gleich große 120°-Sektoren, von denen zwei Sektoren die Ziffer 1, ein Sektor die Ziffer 2 trägt.

Nun drehen zwei Spieler A und B das Glücksrad je einmal. Sind die beiden gedrehten Ziffern gleich, so gewinnt Spieler A und erhält 2 € von Spieler B. Andernfalls gewinnt Spieler B und erhält die Ziffernsumme in € von Spieler A. Welcher Spieler ist im Vorteil.

P(1I1)=1/9

P(1I1)=1/9

P(1I1)=1/9

P(1I1)=1/9

P(2I2)=1/9

P(Gewinn für Spieler A)=5/9

Gewinn=5/9 * 2€=10/9

Wie geht das weiter.?

Answer 1

Der Anfang war schon mal sehr gut:

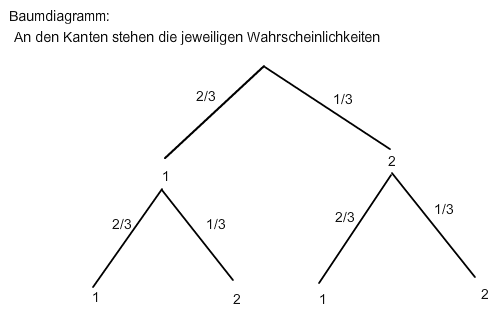
P("2 gleiche Zahlen") = 2/3 * 2/3 + 1/3 * 1/3 = 5/9

P("2 verschiedene Zahlen") = 2/3*1/3 + 1/3*2/3 = 4/9           [ = 1 - 5/9 ]

Für die Erwartungswerte für den Gewinn bei einem Spiel gilt:

E(A) = 5/9 • 2€ - 4/9 • 3€ = -2/9 €

E(B) = 4/9 • 3€ - 5/9 • 2€ =  2/9 €

→  B ist im Vorteil  (zumindest auf Dauer bei mehreren Spielen)

Oder:

B gewinnt im Durchschnitt 4 von 9 Spielen und erhält dafür 4•3€ = 12€ von A

A gewinnt im Durchschnitt 5 von 9 Spielen und erhält dafür 5•2€ = 10€ von B

Gruß Wolfgang

Comments

Dankeschön, ich hatte ein falches Baumdiagramm gezeichnet

---

Ich habe eine Frage,

die Ziffersumme ist doch eigentlich für ... 6, weil für P(2I1) und P(1I2) ... 3+3=6?

P("2 verschiedene Zahlen") = 2/3*1/3 + 1/3*2/3 = 4/9           [ = 1 - 5/9 ]

---

Das Rad wird 2-mal (von jedem 1-mal) gedreht.

Bei 2 verschiedenen Zahlen ist die Ziffernsumme immer 1+2=3

---

Ich weiß, ich meine eigentlich:

P("2 verschiedene Zahlen") = 2/3*1/3 + 1/3*2/3 = 4/9         

Ich kann hier einmal eine 2 und dann eine 1 drehen & zuerst eine 1 dann eine 2.

das wäre doch theoretisch 2+ 1                                   +                            1 + 2=6

---

Das verwechselt du. Gedreht wird nur zweimal und diese Augensumme ist gemeint. Nicht die, die sich bei verschiedenen Drehmöglichkeiten insgesamt ergibt.

---

wenn jemand Interesse zeigt, macht man das gern :-)