Hallo Sonnenschein,
f (x)=1/9x5 - 20/27 x4 + 10/9x3
f '(x) = 5/9 x4 - 80/27 x3 + 10/3 x2
f '(x) = 0 ⇔ x2 • (5/9 x2 - 80/27 x+ 10/3) = 0
x1=0 doppelt → Sattelpunkt
x = 1.612574113 mit Vorzeichenwechsel + → - (Gipfel)
x = 3.720759220 mit VZW - → + (Tal)
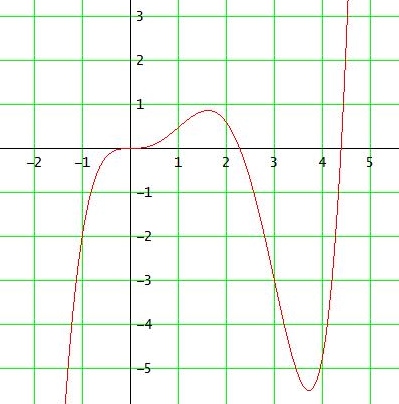
f(1,61) ≈ 0.8619061792 → Gipfelpunkt ≈ (1,91 | 0,86)
f(3,72) ≈ -5,5 → Talpunkt ≈ (3,72|-5,5)
Gruß Wolfgang