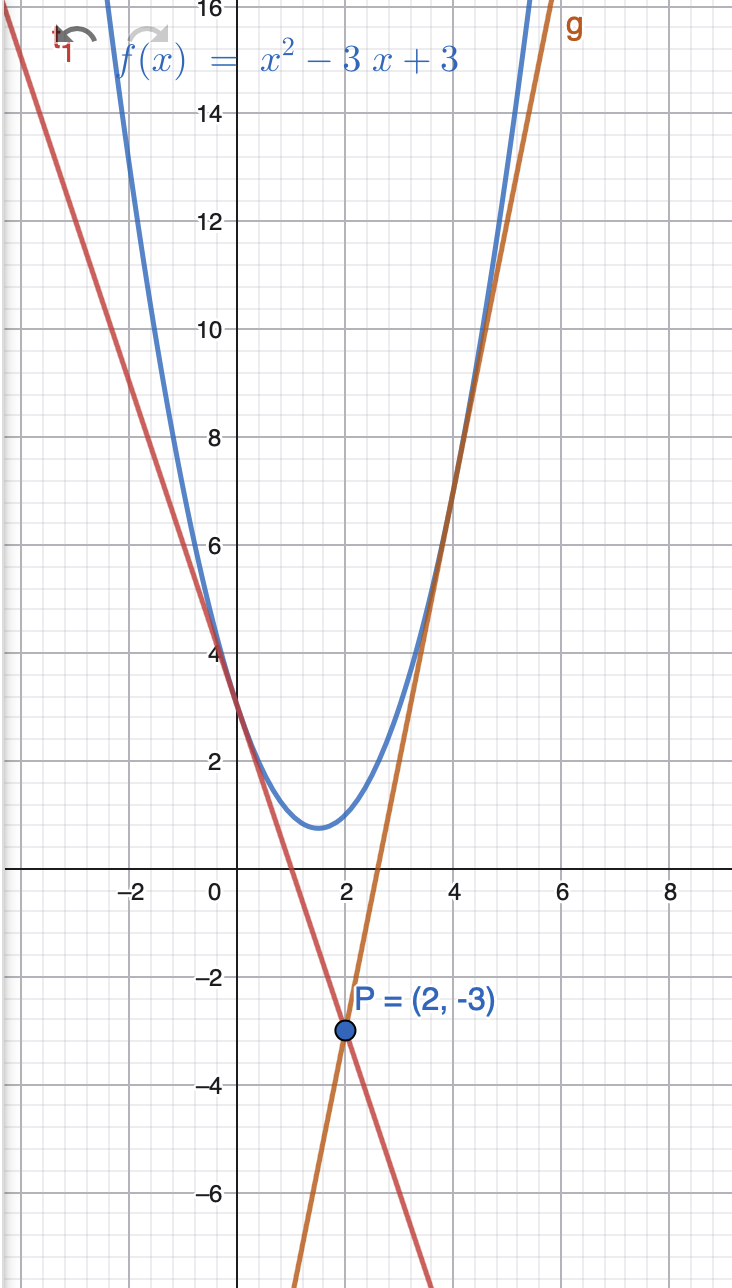
Punkt P(2|-3) liegt nicht auf Kurve von \(f(x)=x^2-3x+3 \). Wie lauten die Tangenten?
Ohne Ableitung:
Geradenschar durch P(2|-3):
\( \frac{y+3}{x-2}=m\) →\( y=mx-2m-3\). Schnitt mit f:
\(x^2-3x+3=mx-2m-3 \) Umstellen:
\(x^2-3x-mx=-2m-6 \) x ausklammern:
\(x^2-x(3+m)=-2m-6 \) quadratische Ergänzung: \( +( \frac{3+m}{2})^2 \)
\(x^2-x(3+m)+( \frac{3+m}{2})^2 =-2m-6+( \frac{3+m}{2})^2 \) 2. Binom:
\((x- \frac{3+m}{2})^2 =\frac{m^2-2m-15}{4}|±\sqrt{ } \)
\(x- \frac{3+m}{2} =\sqrt{\frac{m^2-2m-15}{4}} \) Nun den Term unter der Wurzel =0 setzen
\(m^2-2m-15=0 \)
\(m_1=-3\) oder \( m_2=5 \)
1.Tangente:
\( y=mx-2m-3\) →\( y=-3x+3\).
2.Tangente:
\( y=5x-13\)