Das Dreieck sieht ja so aus:
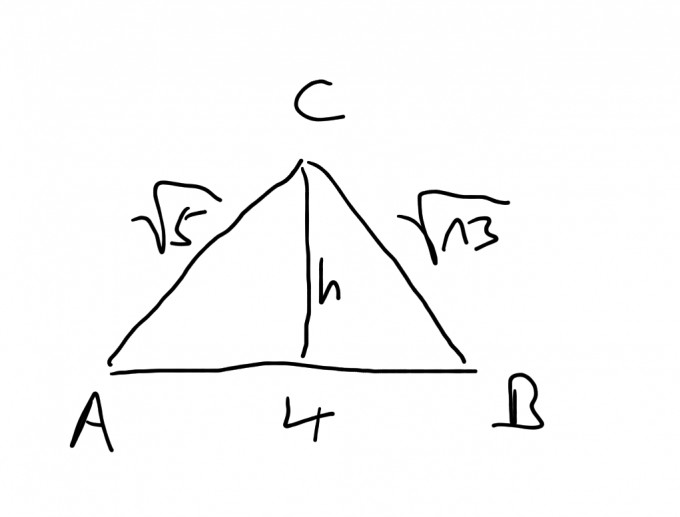
Du hast also 3 Seiten gegeben. Für die Fläche brauchst du die Höhe. Um diese auszurechnen kannst du mit dem kosinussatz den Winkel alpha bestimmen.
Alpha=arccos ((a^2-b^2-c^2)/(-2*bc))
Ergibt mit Zahlen eingesetzt alpha=63,43°.
Die Höhe bestimmst du nun mit dem Sinus. Es ergibt sich h=2.
Damit ist die Fläche A=4*2/2=4.
Falls du noch fragen hast, melde dich!