Hallo Astrid,
f(x) = (x2 + 1) / x
die Ableitungen bestimmst du mit der Quotientenregel [ u / v ] ' = ( u' * v - u * v' ) / v2
f '(x) = (x2 - 1) / x2
f "(x) = 2 / x3
1) maximaler Definitionsbereich
Der Nenner darf nicht 0 werden → D = ℝ \ { 0 }
2) Symmetrie
f(-x) = ( (-x)2 + 1) / (-x) = ( x2 + 1 ) / (-x) = - (x2 + 1) / x = - f(x)
→ Symmetrie zum Ursprung
3) Nullstellen:
f(x) = 0 ⇔D x2 + 1 = 0 → keine Nullstellen
4) Verhalten an den den Randstellen des Definitionsbereichs
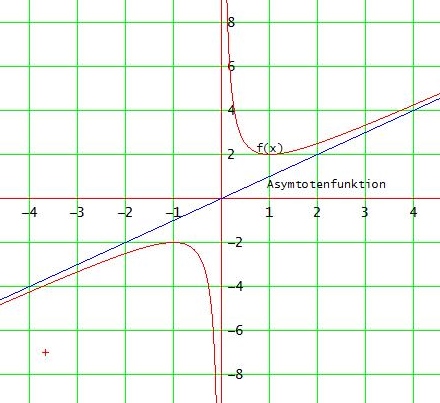
f(x) = x + 1/x → Asymptotenfunktion fA(x) = x
limx→±∞ f(x) = ± ∞
[ Asymptotenfunktion, der sich f im Unendlichen nähert ]
5) Extremwerte und Monotonie:
f '(x) = 0 ergibt die möglichen Extremstellen xE
(x2 - 1) / x2 = 0 ⇔ x2 - 1 = 0 ⇔ x = ± 1
x1 = 1 ; f " (1) = 2 > 0 → T(1| 2)
x2 = -1 ; f "(-1) = -2 → H(-1| -2)
f ist also streng monoton steigend in ] - ∞ , -1 ] und in [ 1 ; ∞ [ , sm-fallend in [ -1 , 1 ]
6) Wendepunkte und Krümmung:
f " (x) = 0 ergibt die möglichen Wendestellen xw
2/x3 hat keine Nullstellen → keine Wendepunkte
f "(x) > 0 ⇔ x>0 → Linkskrümmung in ℝ+ , RK in ℝ-
7) Verhalten an der Definitionslücke:
x=0 ist eine Polstelle mit Vorzeichenwechsel:
limx→0+ f(x) = limx→0+ ( x + 1/x ) = ∞
limx→0- f(x) = limx→0- ( x + 1/x ) = - ∞
8) Graph:
#) Es heißt Asymptotenfunktion :-)
Gruß Wolfgang