Die symbolische Skizze zeigt dir die Zusammenhänge
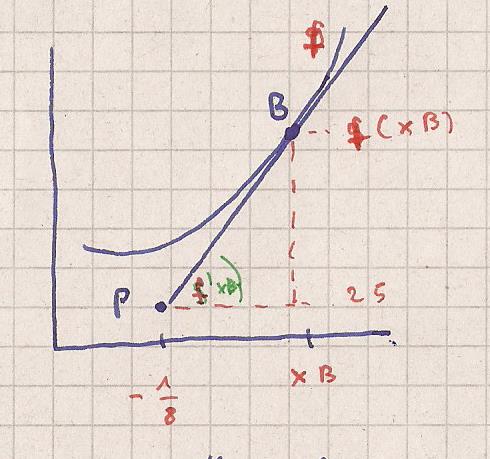
Die Gerade P nach B ist die Tangente
Die Tangente hat dieselbe Steigung wie die Funktion f
im Berührpunkt B
Die Steigung ist Δ y / Δ x = ( f (xB) ) - 25 ) / ( xB - ( -1/8 )
Die Steigung im Berührpunkt ist f ´( xB)
Also
f ´( xb ) = ( f (xB) ) - 25 ) / ( xB - ( -1/8 )
Dies sind die grundsätzlichen Zusammenhänge.
Geht noch weiter.