Vom Duplikat:
Titel: Mathematik Problem 11. Klasse
Stichworte: ableitung,allgemein,differenzenquotient
Text erkannt:
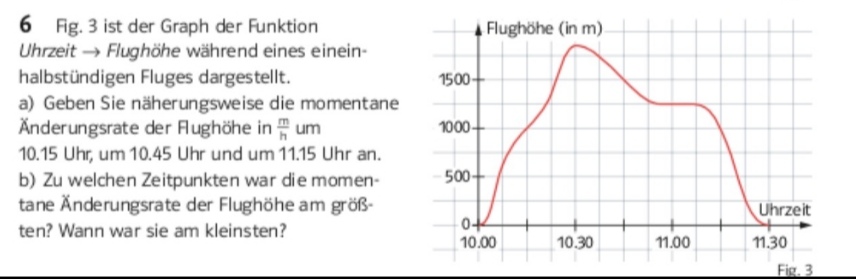
6 Fig. 3 ist der Graph der Funktion Uhrzeit \( \rightarrow \) Flughöhe während eines einein
halbstündigen Fluges dargestellt.
a) Geben Sie näherungsweise die momentane Ánderungsrate der Aughöhe in \( \frac{m}{n} \) um 10.15 Uhr, um 10.45 Uhr und um 11.15 Uhr an.
b) Zu welchen Zeitpunkten war die momentane Anderungsrate der Flughöhe am größ ten? Wann war sie am kleinsten?
Aufgabe:
Ich verstehe nicht wie man diese Aufgabe machen soll... Also was muss ich machen? Worum es geht genau? Und wie löst man die Aufgabe? Also mit h-Methode, Differenzenquotient, oder was weiß ich... Und so weiter
Problem/Ansatz:
Könnte jemand mir bitte helfen?