Bestimmen sie die kleinste natürliche Zahl k, für welche f(x)=x^4+x-9 auf dem Interval (k, k+1) eine Nullstelle besitzt.

Question

die Aufgabe lautet:

Bestimmen sie die kleinste natürliche Zahl k, für welche f(x)=x^4+x-9 auf dem Interval (k, k+1) eine Nullstelle besitzt.

Wie gehe ich an diese Aufgabe heran? Ich habe leider keine Ahnung, was ich bei dieser Aufgabe tun soll...

LG

Comments

Tipp: ƒ(1) < 0, ƒ(2) > 0.

Answer 1

f ' (x) = 3x³ + 1    Das ist für x>0  positiv , also f für x >0  streng monoton steigend.

Und f(2) = 9 > 0   und  f ( 1 ) = -7  < 0 .

Also ist   k=1 .

Comments

Warum fallend?

---

es tut mir leid, aber das ging mir leider zu schnell.

Wie komme ich darauf 1 und 2 einzusetzen? Durch ausprobieren oder woran erkenne ich das?

---

Also fallend war Quatsch, sollte natürlich steigend heißen
(wird korrigiert).
Und wenn dann f(0) und f(1) beide negativ sind, kann es wegen der

Monotonie keine Nullstelle dazwischen geben.

f(2) ist aber nun positiv, also muss zwischen 1 und 2

irgendwie die x-Achse geschnitten werden, also

ist k=1 die gesuchte Zahl.

Answer 2

Bestimmen sie die kleinste natürliche Zahl k,
für welche f(x)=x⁴+x-9 auf dem Interval (k, k+1)
eine Nullstelle besitzt.

Wie gehe ich an diese Aufgabe heran? Ich
habe leider keine Ahnung, was ich bei dieser
Aufgabe tun soll...

Du sollst nachsehen ob im Intervall
1 bis ( 1 + 1 ) eine Nullstelle der Funktion ist
1 .. 2
oder im Intervall
2 .. 3
oder im Intervall
3 .. 4

Nullstellen können mit dem Newton-Verfahren
bestimmt werden
oder es wird nachgeschaut
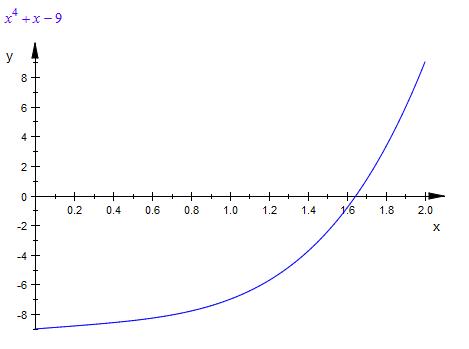
f ( 1 ) = -7
f ( 2 ) =  9
f ( 3 ) = 75

Zwischen 1 und 2 wechselt das Vorzeichen
des Funktionswerts

Antwort : die kleinste natürliche Zahl ist
k = 1.

mfg Georg

Comments

Ich meine ja, das Argument "Monotonie" gehört doch dazu; denn

sonst könnten ja theoretisch zwischen 0 und 1 auch eine Nullstelle

(oder womöglich 2) sein.

---

hey, vielen dank für diese ausführliche Antwort, das hat auf jeden Fall geholfen! :)

---

Hallo mathef,

gehört die 0 noch zu den natürlichen Zahlen ?
Sonst bräuchte man erst bei x = 1 zu beginnen

und der Monotonienachweis könnte entfallen.