Schubkurbel: Gesucht sind die Komponenten der Geschwindigkeit

Question

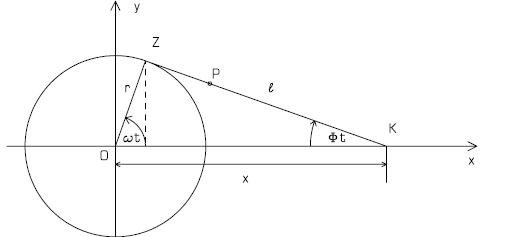
Aufgabe 1: Formel eines Schubkurbelgetriebes

Ist bei einem Schubkurbelgetriebe (s. Skizze) die Kurbellänge \( \mathrm{r} \) sehr klein im Vergleich zur Schubstangenlänge \( \ell \), so gilt für die Abszisse des Kreuzkopfes \( \mathrm{K} \) näherungsweise:

\( \mathrm{x}(\mathrm{t}) \approx \frac{\left.4\right|^{2}-\mathrm{r}^{2}}{4 \mid}+\mathrm{r} \cos \omega \mathrm{t}+\frac{\mathrm{r}^{2}}{4 \mid} \cos 2 \omega \mathrm{t} \qquad (t \geq 0) \).

(i) Diese Formel ist unter Verwendung der Beziehung \( \sqrt{1-\varepsilon} \approx 1-\frac{1}{2} \varepsilon \quad(\varepsilon<<1) \) und trigonometrischer Beziehungen zu bestätigen.

Aufgabe 2:

Der Punkt P teile die Schubstange ZK im Verhältnis m:n. Wie groß sind Horizontal- und Vertikalkomponente seiner Geschwindigkeit ? (Hinweis: Strahlensatz)

Comments

Wie genau verläuft die Bewegung der Schubstange?

Z bewegt sich auf dem Kreis und K auf der x-Achse?

Omega und Phi können nicht beide linear von t abhängen?

Soll sich Z in einer gleichförmigen Kreisbewegung befinden?

Answer 1

x = x_r  + x_L;

x_r = r*cos(ωt);
h = r*sin(ωt);
x_L = sqrt(l^2 -h^2) = sqrt( l^2 -r^2 sin^2(ωt) );  //aus Pythagoras

x_L = l*sqrt{ 1 -r^2/l^2 * sin^2(ωt) }; //da r << l  gilt Beziehung (i)

x_L ≈ l * { 1 -1/2 *r^2/l^2 *sin^2(ωt) };  //sin^2(ωt) = 1/2 *{1 -cos(2ωt) };

x_L ≈ l * { 1 -1/2 *r^2/l^2 *[1 -cos(2ωt)] };

x_L ≈ l -r^2/(4*l) +r^2/(4*l) *cos(2ωt) } = (4*l^2 -r^2) / (4*l) +r^2 / (4*l) *cos(2ωt);

 

x ≈ r*cos(ωt) +(4*l^2 -r^2) / (4*l) +r^2 / (4*l) *cos(2ωt);