gebe ich der erste Figur den Index 0, so kommen in jedem Schritt \(3^{(n-1)}\) kleine Quadrate hinzu. Jedes dieser Quadrate hat die Seitenlänge \(a \cdot 3^{-n}\) - also das zusätzliche Quadrat bei der zweiten Figur (\(n=1\)) hat die Seitenlänge \(a/3\), die Quadrate bei der nächsten haben \(a/9\) usw. Der Umfang \(U\) berechnet sich aus der Summe von \(a^2\) und aller zusätzlichen senkrechten Seiten. \(a\) sei die Seitenlänge des ursprünglichen Quadrats. Da jedes zusätzliche Quadrat zwei senkrechte Seiten hat - folgt daraus
$$U_n=U_{n-1} + 2 \cdot 3^{(n-1)} \cdot a\cdot 3^{-n}=U_{n-1} + \frac{2}{3}a$$
D.h. der Umfang wächst mit jedem Schritt um einen konstanten Betrag und damit über alle Grenzen - es existiert kein Grenzwert.
Die Fläche \(F\) dagegen
$$F_n = F_{n-1} + 3^{(n-1)} \cdot (a \cdot 3^{-n})^2=F_{n-1} + \frac{1}{3^{(n+1)}}a$$
hat einen Grenzwert, da der Zuwachs einer geometrischen Reihe mit einem Faktor \(<1\) entspricht. Das kann man sich anschaulich klar machen, wenn man folgende Figur betrachtet:
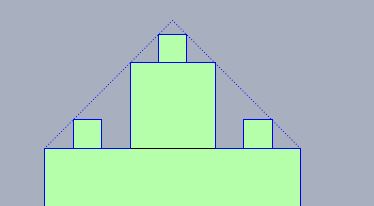
egal wie viele Quadrate noch hinzugefügt werden, sie werden nie über die gepunktete Linie kommen. Der Flächeninhalt ist demnach endlich.
Gruß Werner