Bogen über Seite eines gleichseitigen Dreiecks

Question

Zeige: Für jeden Punkt P auf dem Umkreisbogen über AB des gleichseitigen Dreiecks ABC gilt |PA|+|PB|=|PC|.

Comments

Meinst Du jetzt einen Umkreis um das Dreieck ABC oder einen Kreisbogen über der Strecke AB? Beim Umkreis musst Du doch P nur auf C setzen um das zu widerlegen? :P Gilt wohl nur Für P = A oder P = B?!

Answer 1

Hallo Roland,

es existiert kein Punkt \(P\) für den der Zusammenhang \(|PC|=|PA|+|PB|\) gilt. Schaut man sich folgende Skizze an:

Sei \(e\) ein beliebiger Wert und der blaue Kreis die Menge aller Punkte, die von \(C\) den Abstand \(e\) haben und die rote Ellipse die Menge aller Punkte, deren Abstandsumme von \(A\) und \(B\) ebenfalls identisch zu \(e\) ist, so müsste ein Punkt \(P\), der obigen Bedingung erfüllt, auf einem der Schnittpunkte von Kreis und Ellipse liegen. Und wenn es so einen Schnittpunkt gibt, dann sollte augenscheinlich die Strecke \(|CT|\) größer sein als \(e\) (der Radius des Kreises).

Es muss also gelten (\(s\) ist die Seitenlänge des Dreiecks)

$$\frac12 \sqrt{3} s + \frac12 \sqrt{e^2 - s^2} \gt e$$

Diese Bedingung ist aber für Verhältnisse von \(\frac{e}{s} > 0\) nicht erfüllbar.

Gruß Werner

Edit: die Folgerung hier ist falsch; siehe Kommentar unten

Comments

Hi Werner,

kannst Du mir gerade mal auf die Sprünge helfen? Wenn e = s ist, sollte die Bedingung doch erfüllt sein? Denn wenn bspw P = A, dann haben wir doch |PA|+|PB| = 0 + |PB| = |PC|

Das krieg ich aber mit Deinem Bsp nicht hin.

Grüße

---

Richtige Skizze :

---

Hi Unknown und alle,

Ich hatte vorhin zunächst die gleiche Skizze erstellt, die auch hj2166 gezeichnet hat. Und beim Nachmessen ging die Summe nicht auf - ich weiß nun nicht mehr warum. Und da nicht klar war, was Roland mit 'Umkreisbogen über AB' meinte (s.a. Unknowns Kommentar unter der Frage), so stellte ich mir die umgekehrte Aufgabe irgendeinen Punkt zu finden, der diese Summe erfüllt. Und irgendwie bekam ich es nicht hin und begann nachzurechnen (s. meine Antwort). Die anscheinende Lösung war: keine Lösung. Da ich mir unsicher war, habe ich das mit WolframAlpha nachgerechnet - auch keine Lösung. Und dann war ich in Zeitdruck und habe obige Antwort raus gehauen.

Mein Fehler war, dass ich von zwei Schnittpunkten ausgegangen bin. Es liegen aber zwei Berührpunkte vor. Und die Gleichung muss genauer

$$\frac12 \sqrt{3} s + \frac12 \sqrt{e^2 - s^2} \ge e$$

heißen (man beachte das \(\ge\) ) und dann besitzt sie tatsächlich eine singuläre(!) Lösung bei \(\frac{e}{s}=\frac23 \sqrt{3}\) (scheint selbst hj2166 nicht gesehen zu haben)

Nun noch zu Unknowns Frage: Ich betrachtete in meiner Antwort nicht die Fälle \(P=A\) oder \(P=B\), sondern nur den Fall, für den \(P\) auf der Mittelsenkrechten von \(AB\) liegt.

Und zum Abschluss noch die Konstruktion mit den Berührpunkten:

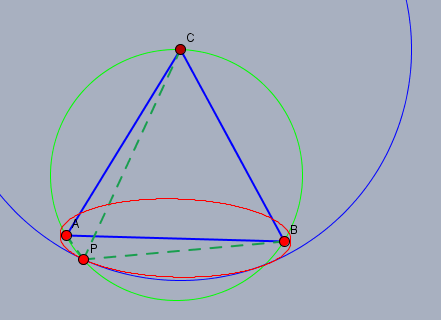
Wenn man genau den richtigen Radius \(|PC|\) wählt, so berührt die rote Ellipse den blauen Kreis. Für jeden anderen Radius liegt die Ellipse innerhalb des Kreises!

So - jetzt brauchen wir immer noch einen Beweis - mathef hat ja schon einen Vorschlag gemacht ...

Gruß Werner

---

Und kaum denke ich über eine (geometrischen) Beweis nach - schon hab' ich ihn ;-)

Ich spiegele zunächst den Punkt \(A\) an \(BC\) und erhalte den Punkt \(B'\). Dann bekommt man ein zweites gleichseitiges Dreieck \(BB'C\) mit gleicher Seitenlänge und Umkreismittelpunkt \(M'\). Der Winkel \(PCA\) (gelb) ist identisch zu \(PBA\), da Umfangswinkel. Nach dem Sehnentangentenwinkelsatz ist der Scheitelwinkel von \(PBA\) identisch zum Winkel \(P'CB\) (Gerade durch \(AB\) ist Tangente am Umkreis um \(M'\)). Da die beiden Umkreise (grün) gleiche Radien haben muss dann auch nach der Umkehrung des Umfangswinkelsatz die Strecke \(|BP'|\) identisch zu \(|AP|\) sein.

Auf Grund der Gleichheit der Winkel \(PCA\) und \(P'CB\) muss der Winkel \(P'CP=60°\) betragen. Der Winkel \(CPB\) ist ebenso \(60°\) da Umfangswinkel zu \(CAB\). Folglich ist das Dreieck \(PP'C\) ein gleichseitiges und die Strecken \(|PP'|\) und \(|PC|\) sind gleich lang. Und \(|PP'|= |PB| + |BP'| = |PB|+|AP|=|PC|\).

q.e.d. Gruß Werner

Answer 2

Da fehlt wohl - wie in der richtigen Skizze ersichtlich - die Bedingung

P liegt auf dem C gegenüberliegenden Umkreisbogen .

Da kann man ja etliche Gleichungen aufstellen, etwa mit dem 

Kosinussatz unter Verwendung von des Satzes vom Mittelpunktswinkel.

Wenn ß der Umfangswinkel zur Sehne AP ist und a die Dreiecksseite

also a=r*√3  gilt z.B. in APC 

AP² = 3r² + PC² - 2r*√3 *PC*cos(ß)   und in APM 

AP² = r² + r² - 2r²*cos(ß)

entsprechendes geht ja wohl auch PBC und PBM und 

bei APB ist ja der Winkel bei P wohl 120°, also auch

3r² = AP² + PB² - 2 AP*PB*cos(120°)

und vielleicht lässt sich da was draus machen ???