Vorwort:
Der Artikel dient der Ausdehnung der Informationsübermittlung des mathematischen Spektrums auf der Mathelounge.
Gerolamo Cardano war ein italienischer Arzt, Philosoph und Mathematiker. Die Cardanischen Formeln wurden erstmals 1545 in seinem Buch "Ars magna" veröffentlicht, was soviel heißt wie: "Die Kunst der großen Dinge".
Da wie ich finde, es am Effektivsten ist anhand eines Beispiels die Anwendung und den Zweck der Cardanischen Formeln zu erläutern, werde ich nun einen Sachverhalt schildern, welcher mit den Formeln gelöst werden kann.
Anwendungsbeispiel:
Wie sieht so eine Gleichung überhaupt aus?
Die allgemeine Gleichung dritten Grades (Kubische Gleichung) lautet wie folgt:
$$ Ax^3+Bx^2+Cx+D=0 $$Kommen wir nun, zu unserem frei-erfundenen Anwendungsbeispiel:
$$ 3x^3+21x^2+3x-45=0$$Da es sich bei dieser Gleichung nur um reelle Zahlen handelt kann man durch Division von "A" ,die Funktion zunächst in die Normalform bringen:$$ x^3+ax^2+bx+c=0$$ Übertragen wir dieses Schema auf unser Beispiel:$$ x^3+7x^2+1x-15$$
Vorbereitungen vor der Formeleinsetzung
Da wir nun eine Funktion haben, deren Anforderungen der Cardanischen Formel entsprechen, müssen wir nun jedoch noch einige Vorbereitungen abschließen.
Wir müssen das quadratische Glied beseitigen. Das geht am besten mit der Substitution:$$ x=z-\frac{a}{3} $$ Dadurch erhalten wir eine reduzierte Form der Gleichung:$$ z^3+pz+q=0 $$ Nun sind wir schon bei der ersten Formel angekommen. Wir müssen vorab das "p" und das "q" der reduzierten Funktion ausrechnen. Das tun wir wie folgt:$$ p=b-\frac{a^2}{3}\quad und \quad q=\frac{2a^3}{27}-\frac{ab}{3}+c $$ Mit diesen im Hinterkopf, können wir nun unser Anwendungsbeispiel dort hineinsetzen (Aufpassen, hier muss die Normalform benutzt werden):$$ p=1-\frac{7^2}{3}=-\frac{46}{3}\quad und \quad q=\frac{2\cdot 7^3}{27}-\frac{7\cdot 1}{3}+(-15)≈8.074$$
Wie viele verschiedene Schnittstellen haben wir an der X-Achse?
Diese Frage kann man sich ganz einfach mit einer leichten Formel beantworten:$$ Δ=(\frac{q}{2})^2+(\frac{p}{3})^3 $$Setzen wir unsere Werte dort ein: $$ Δ=(\frac{8.074}{2})^2+(\frac{-\frac{46}{3}}{3})^3≈-177.223 $$Hierbei ist zu beachten, dass (D=Δ):
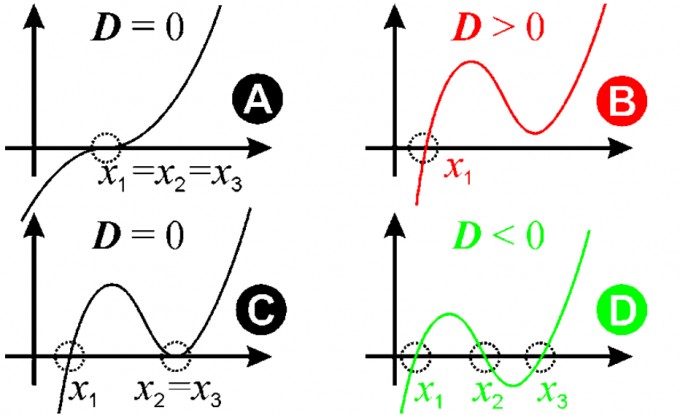
In unserem Beispiel heißt das, dass wir dem grünen Graphen entsprechen und es drei reelle Nullstellen gibt.
Formeleinsetzung und endgültige Nullstellenerrechnung:
Nun kommt der spannendste Part der Cardanischen Formeln. Wir sind bereit alle ausgerechneten Glieder in die Formel einzusetzen. Dafür brauchen wir aber erst einmal alle Formeln:$$ {x}_{1}=\sqrt{-\frac{4}{3}p}\cdot cos(\frac{1}{3}arccos(-\frac{q}{2}\cdot\sqrt{-\frac{27}{p^3}}))-\frac{B}{3A} $$$$ {x}_{2}=-\sqrt{-\frac{4}{3}p}\cdot cos(\frac{1}{3}arccos(-\frac{q}{2}\cdot\sqrt{-\frac{27}{p^3}})+\frac{π}{3})-\frac{B}{3A} $$$$ {x}_{3}=-\sqrt{-\frac{4}{3}p}\cdot cos(\frac{1}{3}arccos(-\frac{q}{2}\cdot\sqrt{-\frac{27}{p^3}})-\frac{π}{3})-\frac{B}{3A} $$ Nun sind wir startbereit und können unsere Werte einsetzen!:$$ {x}_{1}=\sqrt{-\frac{4}{3}\cdot(-\frac{46}{3})}\cdot cos(\frac{1}{3}arccos(-\frac{8.074}{2}\cdot\sqrt{-\frac{27}{(-\frac{46}{3})^3}}))-\frac{21}{3\cdot3}≈1.286$$$$ {x}_{2}=-\sqrt{-\frac{4}{3}\cdot(-\frac{46}{3})}\cdot cos(\frac{1}{3}arccos(-\frac{8.074}{2}\cdot\sqrt{-\frac{27}{(-\frac{46}{3})^3}})+\frac{π}{3})-\frac{21}{3\cdot3}≈-1.797 $$$$ {x}_{3}=-\sqrt{-\frac{4}{3}\cdot(-\frac{46}{3})}\cdot cos(\frac{1}{3}arccos(-\frac{8.074}{2}\cdot\sqrt{-\frac{27}{(-\frac{46}{3})^3}})-\frac{π}{3})-\frac{21}{3\cdot3}≈-6.49$$
Stimmen diese Ergebnisse überhaupt?
Ja, diese stimmen. Wir können, wenn du Zweifel hast diese gerne noch einmal überprüfen:
~plot~ 3x^3+21x^2+3x-45 ~plot~
Fazit:
Insgesamt sind die Cardanischen Formeln sehr aufwendig. Es sind sehr viele Formeln, welche man mühselig in den Taschenrechner eintippen muss. Doch für das Lösen einer kubischen Gleichung finde ich sie doch sehr hilfreich, da sie für mich zumindestens leicht zu verstehen war.