Du schriebst: "Zu dem Rechteck a= 10 LE; b= 5LE; c= 5,59 LE" Du meinst Quader und nicht Rechteck - oder?
Du fragtest: "Das selbe gilt für winkel gamma bei beiden. Was ist daran falsch???" Nichts! das ist richtig. Die Abmessungen des Quaders wurden so gewählt, dass diese Winkel (in etwa) gleich sind. Daher diese etwas 'krumme' Zahl von \(c=5,59 \text{LE}\).
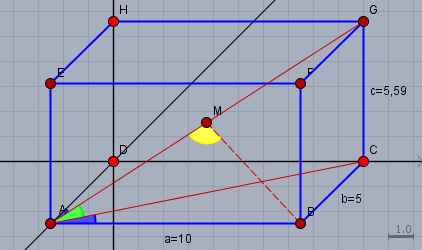
Obige Skizze zeigt den Quader im Schrägriss. Der blaue und grüne Winkel sind in etwa gleich groß.
"2. ich soll den Winkel epsilon (AMB) ausrechnen. Mit M ist der Schnittpunkt der Raumdiagonalen gemeint. Aber welcher winkel ist denn epsilon, in dem entstandenen dreieck gibt es 3 winkel?? Und wie rechne ich das dann aus? " Welcher Winkel epsilon ist, können wir Dir auch nicht sagen, wenn Du uns nicht die vollständige Aufgabenstellung mitteilst, bzw. das zugehörige Bild zeigst. Den Winkel \(\angle AMB\) kann man über den Cosinussatz berechnen. Im Dreieck \(\triangle ABM\) ist die Seite \(AB=a=10\text{LE}\) bekannt. Das Dreieck ist wegen der Symmetrie ein Gleichschenkliges. D.h. \(AM=MB\) und \(AM\) ist die Hälfte der Raumdiagonale \(AG\) und die folgt aus dem Pythagoras:
$$AM=\frac12 AG = \frac12 \sqrt{10^2 + 5^2 + 5,59^2} \approx 6,25$$ Der Cosinussatz im \(\triangle ABM\) für \(\angle AMB\) sagt nun:
$$AB^2 = AM^2 + MB^2 - 2\cdot AM \cdot MB \cdot \cos{(\angle AMB)}$$ $$\begin{aligned} \cos{(\angle AMB)} &= \frac{ 2\cdot AM^2 -AB^2}{ 2 \cdot AM^2}=\frac{2 \cdot 6,25^2 - 10^2}{2 \cdot \colorbox{#ffff88}{6,25}^2} \\ &= \frac{-21,875}{\colorbox{#ffff88}{78,125}} =\colorbox{#ffff88}{-0,28}\end{aligned}$$ $$\Rightarrow \angle AMB \approx \colorbox{#ffff88}{106,3}°$$ Gruß Werner
Edit: Fehler beim Einsetzen korrigiert (gelb markierte Stellen)