zu c.)
Hallo97 hat dir gezeigt wie man die Steigung
( = tan alpha ) über ein Steigungsdreieck
berechnet und dabei immer kleinere Abstände
zwischen x1 und x2 verwendet.
Das kann man über die h-Methode vereinfachen.
h ist der Abstand zwischen x1 und x2
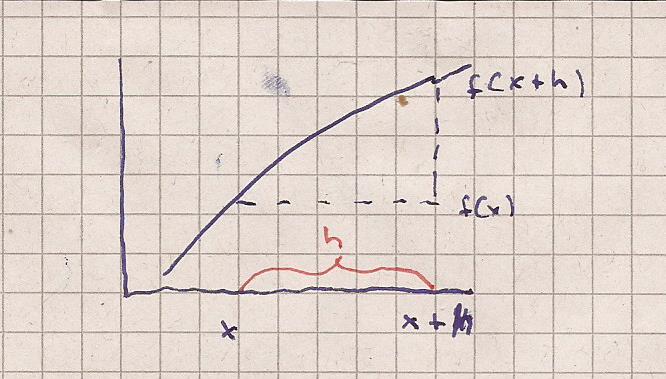
Du hast zwei Punkte
( x | f ( x ) )
und
( x + h | f ( x + h ) )
m = tan ( alpha ) = [ f ( x + h ) - f ( x ) ] / [ ( x + h ) - x ]
Funktionsgleichung in der Normalform
f ( x ) = -0.0066 * x^2 + 0.49 * x
Damit es übersichtlicher bleibt ist
a = -0.0066
b = 0.49
f ( x ) = a * x^2 + b * x
sowie
f ( x + h ) = a * ( x + h ) ^2 + b * ( x + h )
für x = 0 gilt
f ( 0 ) = 0
f ( 0 + h ) = a * ( 0 + h ) ^2 + b * ( 0 + h )
f ( 0 + h ) = a * h^2 + b * h
Oben eingesetzt
m = tan ( alpha ) = [ f ( x + h ) - f ( x ) ] / [ ( x + h ) - x ]
tan ( alpha ) = [ a * h^2 + b * h - 0 ] / h
tan ( alpha ) = [ a * h^2 + b * h ] / h
h ausklammern
tan ( alpha ) = [ h * ( a * h + b ) ] / h
und h kürzen
tan ( alpha ) = ( a * h + b )
h ( der Abstand zwischen den Punkten ) soll
immer kleiner werden und bei 0 ergibt sich
tan ( alpha ) = ( a * 0 + b )
tan ( alpha ) = b
tan ( alpha ) = 0.49
alpha = 26.1 °
Erklärungen
Mit der tan-Funktion wird der Winkel in Grad zum
tan umgewandelt : tan ( 35 ° ) = 0.7
Mit der arctan-Funktion wird der tan in den Winkel in Grad
umgewandelt : acrtan ( 0.7 ) = 35 °.
Der arctan ist also die Umkehrfunktion zur tan-Funktion
arctan ( tan ( alpha ) ) = alpha
Beispiel Quadrat und Wurzel
Wurzei ( x^2 ) = x