Die Frage weist mehrere Ungereimheiten auf.
Jedenfalls für mich.
Jedes Teil wird nacheinander in verschiedenen
Kontrollgängen auf Form, Farbe und Oberflächenbeschaffenheit geprüft.
ich gehe davon aus das jedes Teil 3 Tests durchläuft
und es wird zwischendurch nicht bereits aussortiert.
Ich versuche es zuerst mit einem Venn Diagramm
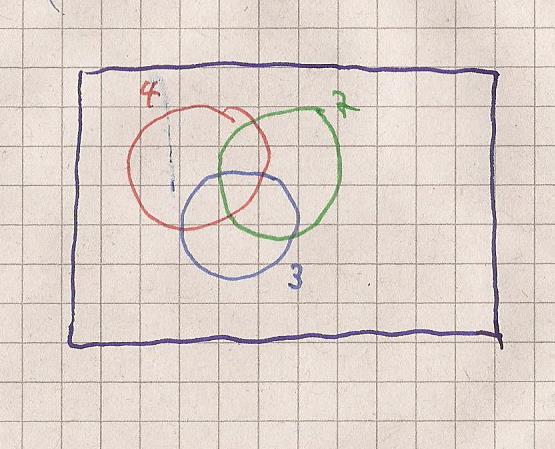
Die Schnittmenge von Rot und grün ist 0.04 * 0.07 = 0.0028 (gr)
Die Schnittmenge von Rot und blau ist 0.04 * 0.03 = 0.0012
Die Schnittmenge von Grün und blau ist 0.07 * 0.03 = 0.0021
Alle drei fehlerhaft ( mittlere Fläche )
0.04 * 0.07 * 0.03 = 0.000084 ( grb )
Jetzt müßte gerechnet werden.
c.)
Rein Rot =
0.04 - ( gr - grb) - ( rb - gbr ) - gbr
0.04 - ( 0.0028 - 0.000084 ) - ( 0.0012 - 0.000084 ) - 0.000084
0.04 - 0.0028 + 0.000084 - 0.0012
0.036084
3.6084 % Rein Rot : nur 1 Formfehler
Dasselbe für Grün und Blau auch ausrechnen
und die 3 Ergebnisse addieren.
Hoffentlich stimmt das alles.