Das ist die Quadratrix des Hippias.
.. und das wird eine Antwort:
Die Parameterform hat Der_Mathechoach schon vorgelegt: $$\begin{pmatrix}x \\ y\end{pmatrix} = \begin{pmatrix}(1 - t)\cdot \tan\left( \frac \pi 2 t \right)\\ 1 - t\end{pmatrix}$$ aus der zweiten Zeile folgt \(t= 1 -y\); das in die erste Zeile einsetzen gibt die Umkehrfunktion: $$x = f^{-1}(y) = y \cdot \tan \left( \frac \pi 2 (1-y)\right)$$
Diese Gleichung stimmt mit der im Wiki-Artikel für \(a=1\) überein: $$f^{-1}(y) = y \cdot \cot \left( \frac \pi {2a} y\right)$$ Die Steigung \(f'(x=0)\) (im Punkt \(P\)) hatte ich im Kommentar schon erwähnt (s.u.): Im Punkt P bewegt sich der Zeiger mit \(\pi/2\) pro Zeiteinheit nach rechts und die Parallele zur X-Achse mit \(1\) pro Zeiteinheit nach unten - macht eine Steigung \(f′(x=0)\) von: $$f'(x=0) = \frac{-1}{\frac\pi2} = \frac{-2}{\pi}$$
Als Goodi noch eine zeichnerische (Näherungs-)Konstruktion der Quadratrix (rot) mittels fortgesetzter Halbierung der Strecke \(OP\) und des Winkels zwischen X- und Y-Achse (Punkte \(A\) bis \(D\)).
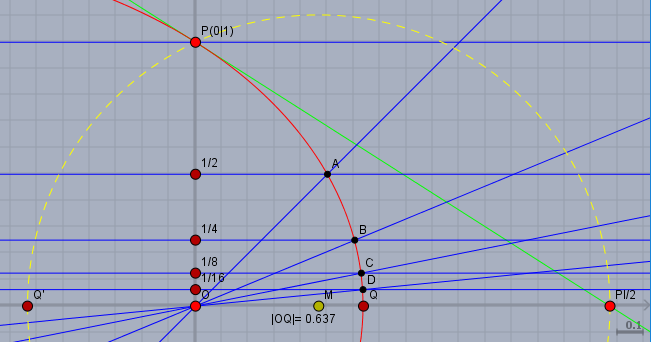
Die Tangente (grün) in \(P\) schneidet die X-Achse bei \(\pi/2\). Spiegelt man den Schnittpunkt \(Q\) der Quadratrix mit der X-Achse am Ursprung \(O\) zu \(Q'\), so liegt \(P\) auf dem Thaleskreis (gelb) über der Strecke \(|Q'(\pi/2|0)|\).
Gruß Werner