Hallo Rosakatze,
die Antwort in Kürze: Bestimme zunächst die Eigenvektoren der Matrix. Diese sind $$e_1= \begin{pmatrix} 1 \\ 1 \end{pmatrix}, \quad e_2 = \begin{pmatrix} 1 \\ -1 \end{pmatrix}$$ \(e_1\) ist der Eigenvektor aus dem Eigenwert \(\lambda_1=1\) und daher auch die Richtung der Spiegelachse. Die Spiegelachse lautet demnach $$g: \space x = \vec{a} + t \begin{pmatrix} 1\\1 \end{pmatrix}$$ und die Gerade setze ich in die Transformationsgleichung ein. Da es sich um eine Verschiebung handelt, sind die Werte für \(t\) für Urbild und Bild unterschiedlich. Ich erwarte dann einen Wert für \(\vec{a}\) zu finden, der die Gleichung erfüllt: $$\vec{a} + t_2 \begin{pmatrix} 1\\1 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ 1& 0 \end{pmatrix} \left( \vec{a} + t_1 \begin{pmatrix} 1\\1 \end{pmatrix} \right) + \begin{pmatrix} 1\\2 \end{pmatrix}\\ (t_2-t_1) \begin{pmatrix} 1\\1 \end{pmatrix} = \begin{pmatrix} -1 & 1 \\ 1& -1 \end{pmatrix} \vec{a} + \begin{pmatrix} 1\\2 \end{pmatrix}$$ Da der Stützpunkt \(\vec{a}\) auf der Spiegelachse frei verschoben werden kann, wähle ich eine der Koordinaten. ich setze \(a_x=0\); es verbleibt: $$(t_2-t_1) \begin{pmatrix} 1\\1 \end{pmatrix} - \begin{pmatrix} \cancel{-1} \, 1 \\ \cancel{1}\,-1 \end{pmatrix} a_y = \begin{pmatrix} 1\\2 \end{pmatrix}\\ t_2-t_1 = \frac32; \quad a_y= 0,5$$ D.h. die Gleichung der Spiegelachse lautet $$g: \space x =\begin{pmatrix} 0\\0,5 \end{pmatrix} + t \begin{pmatrix} 1\\1 \end{pmatrix}$$ und der Gleitanteil führt zu einer Verschiebung von $$\Delta \vec{v} = \frac32 \begin{pmatrix} 1\\1 \end{pmatrix} $$
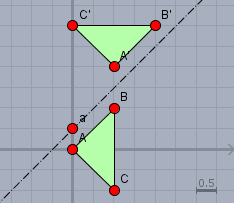
oben in der Skizze habe ich mal die drei Punkte \(A\), \(B\) und \(C\) transformiert. Das Ergebnis bestätigt die Rechnung oben.
Lösung ohne Eigenvektoren:
ich unterstelle im Vorfeld, dass die Spiegelachse nicht parallel zur Y-Achse verläuft - damit kann ich postulieren, dass es einen Punkt \(\vec{a}=(0|a_y)\) gibt, der auf der gesuchten Spiegelachse liegt. Weiter nehme ich an, dass es eine Gleitspiegelung ist und somit einen Vektor \(\vec{v}\) gibt, der für die Verschiebung der Gleitspiegelung sorgt. Daraus folgt nun, dass jeder Punkt \(\vec{x}\) der Form
$$\vec{x} = \vec{a} + t \vec{v} $$
erstens auf der Spiegelachse liegt, da \(\vec{v}\) parallel zu derselben verläuft und zweitens auf
$$ \vec{a} + t \vec{v} \quad \mapsto \quad \vec{a} + t \vec{v} + \vec{v} = \vec{a} + (t +1)\vec{v}$$ abgebildet wird; und dies unabhängig vom Wert von \(t\)! Das setzte ich in die Abbildung ein: $$ \vec{a} + (t +1)\vec{v} = \begin{pmatrix} 0 & 1 \\ 1 & 0\end{pmatrix} \left( \vec{a} + t \vec{v}\right) + \begin{pmatrix} 1\\ 2\end{pmatrix}$$ Und löse es nach den beiden Gleichungen für die Koordinate X und Y auf: $$\begin{aligned} 0 + t v_x + v_x &= a_y + tv_y + 1 \\ a_y + tv_y + v_y &= 0 + tv_x + 2\end{aligned}$$ aus der zweiten Gleichung folgt: $$ \begin{aligned}a_y &= tv_x + 2 - tv_y - v_y \\ a_y &= t(v_x-v_y) + 2-v_y\end{aligned}$$ Oben habe ich vorausgesetzt, dass die Abbildung für jeden Wert von \(t\) gelten muss! \(a_y\) soll aber eine Konstante sein. Daraus folgt, dass \(v_x-v_y=0\) bzw. \(v_x=v_y\) ist. Den Rest setze ich noch für \(a_y\) in die erste Gleichung ein: $$ t v_x + v_x =2 - v_y + tv_y + 1$$ und nun die Werte mit \(t\) nach links und die anderen nach rechts $$\begin{aligned}t v_x - tv_y&= 2 - v_y + 1 - v_x \\ t(v_x - v_y) &= 3 - v_y - v_x\end{aligned}$$ Links steht schon 0, da \(v_x=v_y\) und aus der rechten Seite folgt dann $$0 = 3 - 2v_x \quad \implies v_x = \frac32$$ Einsetzen in die Gleichung für \(a_y\) gibt dann noch \(a_y = 2 - v_y = 2 - \frac32 = \frac12\). Zusammen gefasst lautet die Gleichung für die Spiegelachse der Gleitspiegelung$$g: \space \vec{x} = \begin{pmatrix} 0 \\ a_y \end{pmatrix} + t \begin{pmatrix} v_x \\ v_y \end{pmatrix} = \begin{pmatrix} 0 \\ \frac12 \end{pmatrix} + t \begin{pmatrix} \frac32 \\ \frac32 \end{pmatrix} $$ wobei der Richtungsvektor dieser Geraden auch gleich dem Verschiebevektor der Gleitspiegelung ist.
Darüber hinaus kann man das auch graphisch herleiten:
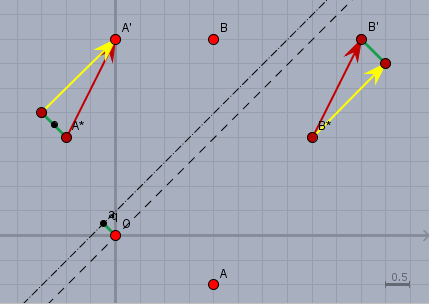
Ich habe dafür beispielhaft beim Punkt \(A\) die Transformation durchgeführt. Ich setze damit voraus, dass bekannt ist, dass die gegebene Matrix zu einer Spiegelung an der Winkelhalbierenden des ersten Quadranten führt. Zunächst also die Spiegelung \(A \mapsto A^*\) an der Winkelhalbierenden des ersten Quadranten und dann die (Gleit)Verschiebung \(A^* \mapsto A'\). Letzteres kann man nun in eine Verschiebung senkrecht zur Spiegelachse (grün) und eine parallel zur Achse (gelb) aufteilen. Aus dem parallelen Anteil (gelb) wird die 'Gleitung' der Gleitspiegelung und der orthogonale Anteil ist zu halbieren, da durch die Spiegelung eine Parallelverschiebung der Spiegelachse zu einer Verdoppelung der Entfernung von Punkt zu Bildpunkt wird. Also formal aufgeteilt in den orthogonalen und parallelen Anteil: $$\begin{pmatrix} 1 \\ 2\end{pmatrix} =2 r\begin{pmatrix} -1 \\ 1\end{pmatrix} + s \begin{pmatrix} 1 \\ 1\end{pmatrix} \\ \implies s = \frac32; \quad r=\frac14$$ So lautet die Gleichung der Spiegelachse $$g: \space \vec{x} = \frac14 \begin{pmatrix} -1 \\ 1\end{pmatrix} + t \frac32 \begin{pmatrix} 1 \\ 1\end{pmatrix}$$ was identisch ist zur obigen Lösung, lediglich mit einem verschobenen Aufpunkt der Geraden.
Gruß Werner