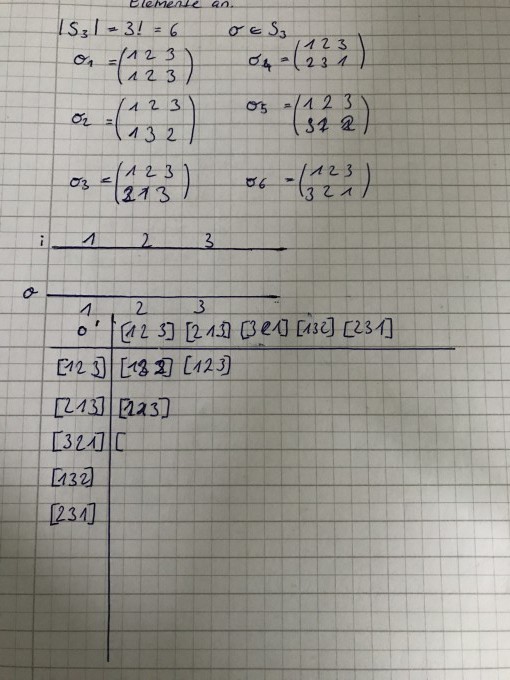Symmetrische Gruppe und Matrizen

Question

Aufgabe:

Die Menge der Permutation auf drei Elementen S₃  = {[123],[213],[321],[132],[231]}

zusammen mit der Verknüpfung  ° , die Hintereinanderausführung der Permutationen bildet eine Gruppe.

a) Stellen Sie die Verknüpfungstabelle von (S₃, °) auf.

b) Geben Sie zu allen Gruppenelementen die inversen Elemente an. 

Problem/Ansatz:

Also erstmal habe ich aufgeschrieben dass |S3| = 3! hat.

Bei der Tabelle war ich mir nicht sicher wie ich herausfinde, welche Gruppe ein neutrales Element haben.

Comments

Oder andere frage, wie berechne ich es?

Das inverse Element muss ja sozusagen das neutrale Element ergeben und das neutrale Element müsste am Anfang der Tabelle stehen, aber mit [123] war ich mir nicht sicher, sonst könnte ja nur das neutrale Element 1 sein bei der Multiplikation. Kann ich dich 1 eigentlich in die Tabelle mit einbeziehen, sodass ich ein neutrales Element habe oder liege ich mit meiner Vermutung völlig falsch?

Answer 1

Wie kommst du denn auf eine 2x3 Matrix?

Habe es eher so verstanden, das [123] jeweils mit [123], [213], [321], [132], [231] verknüpft werden soll, und das Vorzeichen ermittelt werden soll. Also jeweils ob es +1 oder -1 ist. (Siehe Skript S. 387)

Und dann "Die Inverse zu den Gruppenelementen angeben" das +1 in ein -1 änden? (Hier bin ich mir nicht sicher, ob es nicht zu einfach ist?)

Comments

Das Muster kommt mir ein bisschen bekannt vor das mit dem Vorzeichen

A= \( \begin{pmatrix} + & - & + \\ - & + & - \\ + & - & + \end{pmatrix} \)

Ich wahr mir auch nicht sicher, dies das gleiche ist.

Im Buch stand ja folgendes:

sign([123]) = 1, sign([213]) = -1, sign([321]) = 1, sign([132]) = -1, sign([312]) = 1, sign([231]) = -1

Es auf jeden Fall identisch mit der Vorzeichentafel.

---

Ich wahr mir auch nicht so sicher,  dies das gleiche ist

Ich meinte, ich war mir auch nicht so sicher, ob dies das gleiche ist.

Es auf jeden Fall identisch mit der Vorzeichentafel 

Es sieht auf jeden Fall identisch mit der Vorzeichenmatrize aus.

Entschuldigung für nochmal für meine fehlhaften Grammatik  :)

---

Wirf das Buch in die Tonne! Da wird eigentlich nichts weiter versucht als mit möglichst vielen abstrakten Symbolen so viel wie möglich zu verschleiern. Und das nennt sich dann "saubere Darstellung". ;-)

Wenn du die Inverse suchst, nimm einfach die Verknüpfungen aus der Tabelle, in denen [1 2 3], also das neutrale Element rauskommt.

Die Inverse zu 312 ist 231

zu 123 ist 123

zu 213 ist es 213

zu 321 ist es 321

zu 132 ist es 132

zu 312 ist es 231

zu 231 ist es 312

---

Ja das Buch ist überhaupt gar nicht hilfreich  :,D

Genau dass habe gemacht Danke Marceline :)

Answer 2

Also erstmal habe ich aufgeschrieben dass |S3| = 3! hat. Das war überflüssig

Bei der Tabelle war ich mir nicht sicher wie ich herausfinde, welche Gruppe ein neutrales Element haben.

Soll wohl heißen: Bei der Tabelle war ich mir nicht sicher, welches das neutrale Element ist.

Das ist o₁ (das erste oberhalb der angefangenen Tabelle).