Das Verfahren ist lediglich eine Verschmelzung der konventionellen Rechenschritte beim Lagrange-Multiplikator-Verfahren und spart einem in vielen Fällen Zeit. Allerdings nur, wenn die Matrix quadratisch ist – obwohl es auch für nicht-quadratische mit einigen Tricks klappt.
Einfaches, einleitendes Problem zur Demonstration:
(1)
Die Funktion \(f(x,y)=x+y\) soll unter der Nebenbedingung \(x^2+y^2=1 \Longleftrightarrow x^2+y^2-1=0\) optimiert werden.
(2)
Man bilde nun die Determinante und setze sie gleich \(0\):$$\begin{vmatrix} f_x & g_x \\ f_y & g_y \end{vmatrix}\stackrel{!}{=}0$$ Hierbei ist \(f_x=1\), \(f_y=1\), \(g_x=2x\) und \(g_y=2y\). Daraus ergibt sich die Determinante:$$\begin{vmatrix} 1 & 2x \\ 1 & 2y \end{vmatrix}\stackrel{!}{=}0$$ Aufgelöst mit der Regel von Sarrus erhält man:$$2y-2x\stackrel{!}{=}0 \Longleftrightarrow \colorbox{#FFFF00}{y=x}$$ Mittels der Nebenbedingung erhält man nun das Endergebnis:$$x^2+x^2-1=0$$$$2x^2=1$$$$x^2=\frac{1}{2}$$ $$x_{1,2}=y_{1,2}=\pm\frac{\sqrt{2}}{2}$$ (3) Veranschaulichung des Problems:
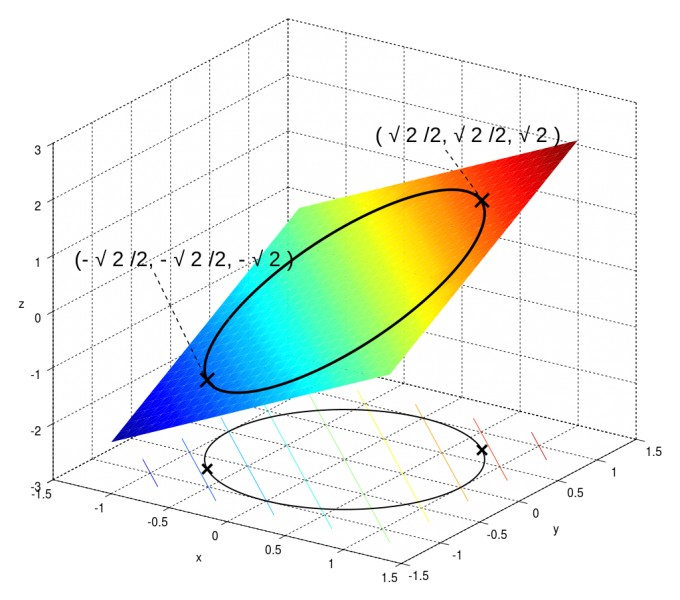
Beispiel, das veranschaulicht, warum sich das Verfahren lohnt:
(1)
Die Funktion \(f(x,y)=e^{-x^-y}\) soll unter der Nebenbedingung \(g(x,y)=x\cdot y\) optimiert werden.
(2)
Die Determinante beläuft sich hier auf \(\begin{vmatrix} -e^{-x-y} & y \\ -e^{-x-y} & x \end{vmatrix}\stackrel{!}{=}0\) Also wieder mit Hilfe von Sarrus:$$-e^{-x-y}\cdot x+e^{-x-y}\cdot y=0$$$$\Longleftrightarrow -e^{-x-y}\cdot (x-y)=0$$ Da die Exponentialfunktion \((e^x)\) niemals \(=0\) werden kann, ist daraus zu deduzieren, dass wieder \( \colorbox{#00ff08}{y=x}\) gilt.
Mit Hilfe der Nebenbedingung belaufen sich die Lösungen auf \( \therefore x=y=0\)
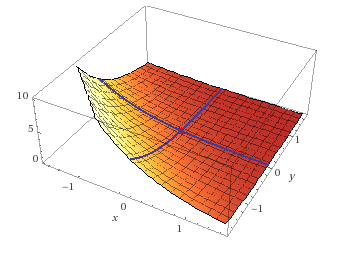
Beispiel mit \(y\neq x\)
Es soll \(f(x,y)=x+20y\) unter der Nebenbedingung \(g(x,y)=\sqrt{x}+y-30\) optimiert werden:$$\begin{vmatrix} 1 & \frac{1}{2\sqrt{x}} \\ 20 & 1 \end{vmatrix}\stackrel{!}{=}0 \Longleftrightarrow 20\cdot\frac{1}{2\sqrt{x}}-1\stackrel{!}{=}0$$$$20\cdot\frac{1}{2\sqrt{x}}-1=0$$$$\therefore x=100$$ Eine Aussage über \(y\) folgt syntaktisch [aus der Nebenbedingung] aus der Aussage über \(x\). Also \(x\vdash y\):$$y=30-\sqrt{100}=20$$ Herleitung:$$\begin{aligned}L &= f + \lambda g \\ L_x &= f_x + \lambda g_x = 0 && \left| \cdot g_y\right. \\ L_y &= f_y + \lambda g_y = 0 && \left| \cdot g_x\right. \end{aligned}$$$$\Longrightarrow f_x g_y - f_y g_x = 0 \Longleftrightarrow \begin{vmatrix} f_x & g_{ x} \\ f_y & g_{ y} \end{vmatrix}=0$$