Lösungsmenge einer Ungleichung bestimmen

Question

Also ich habe die Ungleichung -4/3x² ≥ x und ich muss die Lösungsmenge daraus bestimmen

 

1. Nullstellen berechnen

2. einzeichnen und Lösungsmenge ablesen

Ich weiß nur nicht wie ich diese Ungleichung mit der abc Formel lösen kann, denn mir sind nur Ungleichungen mit einem >0 oder <0 bekannt in diesem Fall steht da ein x

 

wie kann ich da vorgehen?

Answer 1

Annahme x² ist ein Faktor, also nicht unter dem Bruchstrich 

-4/3  x² ≥ x               | + 4/3  x²      

0 ≥ x + 4/3 x²           |x ausklammern

0 ≥ x( 1 + 4/3 x )

2 einfache Nullstellen  x₁ = 0 und x₂ = - 3/4    mit Vorzeichenwechsel

Damit das Produkt nicht grösser als 0 ist, müssen die Faktoren unterschiedliches Vorzeichen haben oder 0 sein.

L={x Element IR  | -0.75 ≤ x ≤0}

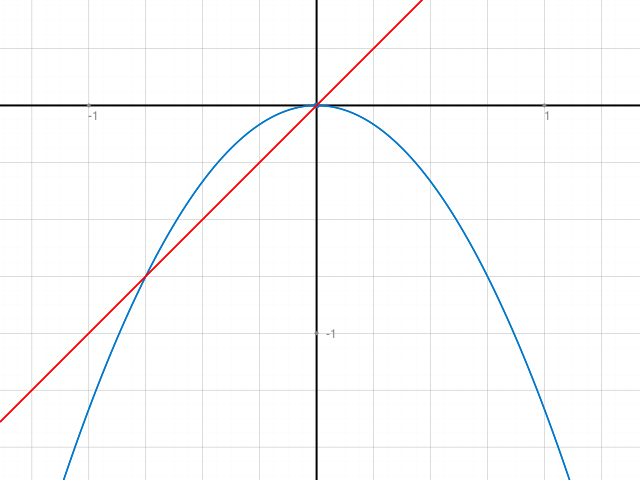
Probe: f(x) = -4/3 x²   und g(x) = x aufzeichnen und schauen, ob die Gerade im angegebenen Bereich unter der Parabel verläuft.

Comments

vielen dank ertmal, kann ich des aber auch so schreiben:

x∈ ]-∞;-0,75[  ∪  ]0; ∞[

geht es oder ist es in diesem Fall falsch?

---

Nein genau dort verläuft die Gerade oberhalb von der Parabel.

Es gilt:

-4/3  x² < x  hat die folgenden Lösungen

x∈ ]-∞;-0,75[  ∪  ]0; ∞[

und 

-4/3  x² ≥ x hat die Lösungen

x∈ [-0,75,0]