Abituraufgabe: Obere Begrenzungslinie des Brückenteils. Was mache ich falsch? Analysis

Question

Aufgabe:

Die Abbildung zeigt das Brückenteil einer Holzeisenbahn.
Die obere Begrenzungslinie des Brückenteils lässt sich durch die Funktion f mit der
Gleichung f(x)=− 1/500*x^3 + 3/50*x^2 +1
beschreiben. 1 LE = 1 cm .

Um Material zu sparen, wird das Brückenteil aus zwei Holzbrettern hergestellt. Das eine Holzbrett wird von den Geraden
g (x)= 45 x−2 und u 100
g (x)= 45 x+1 begrenzt. o 100
Weisen Sie nach, dass der Graph von f für x ∈ [0; 20] vollständig in dem
Bereich liegt, der von den beiden
Geraden g u bzw. g o eingeschlossen wird.
Im Bereich 0 < x < 20 gibt es eine Stelle, an der der vertikale Abstand der Gerade gu zum Graphen von f am geringsten ist. Ermitteln Sie diese Stelle und den minimalen
Abstand.

Aufgabe 1.1. e) : https://bildungsserver.berlin-brandenburg.de/fileadmin/bbb/unterricht/pruefungen/abitur_bb/Zabi_Mathematik/17_Ma_GK_CAS_Aufgaben.pdf

Mein Prozess:

Für den Flächeninhalt von f zwischen 0 und 20 habe ich 100 herausbekommen und mithilfe der Differenzfunktion der beiden geraden bekomme ich nur 60 heraus. Das kann doch nicht stimmen, weil die Antwort größer als 100 sein muss. Was mache ich falsch?

Answer 1

Hier meine Berechnungen

mittlere Steigung 0.4
Bei x = 4.23 und 15.77
Höchste Steigung an der Wendestelle bei x = 10
mit 0.6 bzw. 34.38 °
Differenz zwischen den Tangentensteigungswinkeln
von 0.42 gleich 24.06 °

mfg Georg

Bin bei Bedarf gern weiter behilflich.

Comments

Lieber Herr Born,

vielen, lieben Dank für die Antwort!

Für d hatte ich etwa 21,6 Grad. Wie sind Sie auf 24.06 Grad gekommen? Was haben Sie für e und f herausbekommen?

Ich habe meine Antworten für e und f in den Kommentaren der anderen Antwort eingefügt. Sind diese so richtig?

Liebe Grüße!

---

Hallo Lounger,

Hier die Werte zu d.)

1.) Ableitungsfunktion
2.) Steigung an der Stelle x = 8.5
3.) Steigung in Grad
4.) Steigung an der Stelle x = 1.5
5.) Steigung in Grad
6.) Differenz : 24.06 °

Die anderen Aufgaben kommen später.
mfg Georg

---

e.)
f muß stets unterhalb oder gleich mit g(o) liegen
f muß stets oberhalb oder gleich mit g(u) liegen

Differenzfunktion zu g(o)
g(o) - f = 0.45**x + 1 - ( -1/500 * x^3 + 3/50 * x^2 +1 )
d(o) = 1/500 * x^3 - 3/50 * x^2 + 0.45 * x
max Abstand bei
1.Ableitung, Extremwert
d(o) ´ = 3/500 * x^2 - 6/50 * x + 0.45
3/500 * x^2 - 6/50 * x + 0.45  = 0
x = 5
Funktionswerte bei x = 5
g(o) = 3.25
f = 2.25
g(u) = 0.25
f liegt innerhalb

Differenzfunktion zu g(u)
f - g(u) = -1/500 * x^3 + 3/50 * x^2 +1 - ( 0.45**x -2 )
d(u) = -1/500 * x^3 + 3/50 * x^2 + 1 - 0.45 * x + 2
d(u) ´ = -3/500 * x^2 + 6/50 * x -  0.45 * x
max Abstand bei
1.Ableitung, Extremwert
d(o) ´ = 3/500 * x^2 - 6/50 * x + 0.45
3/500 * x^2 - 6/50 * x + 0.45  = 0
auch bei x = 5
vertikaler Abstand = 2

---

f.)
Ich rechne zunächst die graue Fläche aus
und dann über die Tiefe = Dicke des Bretts
= 4 cm das Volumen.

Gesucht ist die Fläche unterhalb von f sowie
f = -1/500 * x^3 + 3/50 * x^2 +1

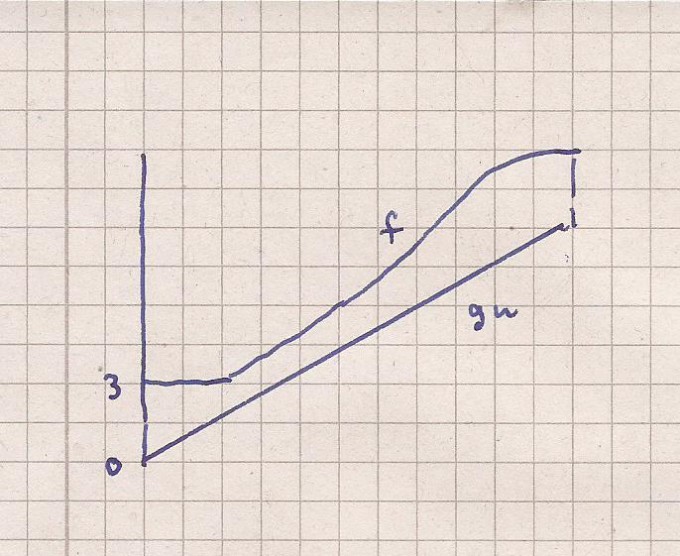
Die beiden Funktionen habe ich um 2 Einheiten nach oben
verschoben um stets im 1.Quadranten beim Integrieren bleiben zu
können.

f = -1/500 * x^3 + 3/50 * x^2 + 3
g(u) = 0.45 * x ( Dreiecksfläche )

S( x ) =-1/500 * x^4 /4 + 3/50 * x^3 / 3 + 3x
F = [ S ] zwischen 0 und 20
F = 100

Dreieckfläche = ( Höhe mal Grundseite / 2 )
( 0.45 * 20 ) * 20 / 2 = 90

100 - 90 = 10

kleines Dreieck
Schnittpunkt mit der x-Achse
g(u) = 0.45 * x - 2
0.45 * x - 2 = 0
x = 4.4444
Fläche
4.4444 * 2 / 2 = 4  4/9

Bisher
10 - 4  4/9 = 5  1/9

graue Fläche rechts als Trapez
[ gu(20)+ gu( 17) ] / 2 * 3
( 7 + 5.65 ) / 2 * 3
18.975

Zusammen
5  5/9 + 18.975

Bitte alles überprüfen.
Etwas komisch kommen mir die Werte für die
Flächen schon vor.

Volumen =  Gesamtfläche * 4 cm = 98.12 cm°3

---

Korrektur
S( x ) =-1/500 * x4 /4 + 3/50 * x3 / 3 + 3x
F = [ S ] zwischen 0 und 20
F = 140

Dreieckfläche = ( Höhe mal Grundseite / 2 )
( 0.45 * 20 ) * 20 / 2 = 90

140 - 90 = 50

minus    4 4/9
plus    18.975

-----------------

64.53 cm^2

---

Vielen, lieben Dank für die ausführliche Hilfe!! :) Sie haben mir sehr weitergeholfen!!

98,12 cm^3 stimmt doch aber nicht, oder?

---

Hallo Lounger,

zur Information :
hier im Forum wird üblicherweise das " du "
verwendet.

Falls die Fläche 64.53 cm^2 ist ist das
Volumen 64.53 * 4 = 258.12 cm^3

Die Flächenberechnung geht auch einfacher:
Fläche unter f :
Int(f,x=0..20 ) = 100
Das helle eingeschlossene Dreieck hat die Maße
Anfang Dreieck ( Nullstelle gu ) 4.4444
Ende Dreieck 17 cm
Grundlinie = 17 - 4.444 = 12.555
Höhe Dreieck bei x = 17 : 5.65
Fläche Dreieck = 12.555 * 5.65 = 35.47

Fläche unter f = 100 minus 35.47 =
64.53 cm^2

Dieselbe Fläche wie oben aber ein bißchen
kürzer berechnet.

Answer 2

Der Flächeninhalt bringt dich nicht wirklich weiter, weil kleine Ausreißer (nach oben) nicht zwingend durch die den Flächenvergleich berücksichtigt werden.

Durch Bilden der Diff.-Funktion \(h(x):=g_o(x)-f(x)=\dfrac{x^3}{500}-\dfrac{3x^2}{50}+\dfrac{9x}{20}\) und dem Nullsetzen dieser \(h(x)=0 \rightarrow x_1=0, \: x_2=15\) lässt sich nun prüfen, welches Vorzeichen die Funktionswerte links und rechts der Nullstellen besitzen:

r. von \(x_1\) bzw. links von \(x_2\): \(f(1)=1.058\)
r. von \(x_2\): \(f(17)=8.514 \)

Also besitzt \(f\) an keiner Stelle auf [0;20] einen größeren Funktionswert als \(g_o\).

Selbiges lässt sich (abgeändert) auch auf \(g_u\) anwenden.

Der geringste Abstand findet sich bei x=5 und beträgt 2cm.

Comments

Vielen Dank! Ich habe die Differenzfunktion gebildet und für Gv= 394,34 cm^3 erhalten. Ist das richtig?

Für den Winkel habe ich 21,65 Grad herausbekommen. (Aufgabe d). Ist das richtig?

---

Für e habe ich:
45.56 FE

---

Wie gesagt, der Flächeninhalt bringt dich nicht weiter. Wo du das Volumen her nimmst, weiß ich nicht.

Ich komme auch in etwa auf 21°.

---

Ich habe den Integral zwischen 0 und 20 berechnet für die Differenzfunktion zwischen f(x) und gu. Das ergab 50. Das habe ich subtrahiert mit dem Flächeninhalt von 4,44 (Flächeninhalt der Gerade zwischen dem Schnittpunkt mit der y-Achse und der x-Achse.)

---

Aufgabe e erfordert doch die Berechnung des Flächeninhalts? So meinte das unser Lehrer vor kurzem.

Für den geringsten Abstand habe ich (5/0,25).

---

Wie bist du auf 21 Grad gekommen? Ich habe die Tangentengleichung gebildet. Die Tangentengleichungen gleichgesetzt und für x x=4,1833 erhalten. Das habe ich in die erste Ableitung eingesetzt und 0,39666 erhalten und daraus den arctan gebildet und 21,6 Grad erhalten.

---

Der Flächenvergleich kann eine notwendige, aber keine hinreichende Bedingung darstellen.

Alternativ könnte man die Aussage mit einer Ungleichung zeigen:

f(x) ≥ g_o bzw. f(x) ≤ g_u

5/0.25 = 20 ist, wie man auch grafisch erkennen kann zu viel.

d_min = |2.25-0.25|=2

---

Ist d)e) und f) somit richtig? Habe ich das richtige Ergebnis?

---

\( \alpha= \arctan \left(\left |\dfrac{0.5865 - 0.1665}{1 + 0.5865\cdot0.1665}\right |\right) \approx 0.3826 = 20.94°\)