Drehkegel mit dem... (Extremwertaufgabe)

Question

Aufgabe:

Einem Drehkegel mit dem Radius r=6 cm und der Höhe h=12 cm ist der volumgrößte Drehzylinder einzuschreiben.

Problem/Ansatz:

Wie groß ist das Volumen des Zylinders?

Für die ausführliche Antwort bin ich sehr dankbar!!!

Answer 1

Extremalbedingung:

V(r,h)=π·r^2·h

Nebenbedingung:

Über Strahlensätze:  h/(R-r)=H/R

hierbei sind H und R die Höhe und der Radius des Kegels, und h,r die des Zylinders.

Answer 2

Hier meine Berechnungen.

Bei Bedarf nachfragen.

Answer 3

Planfigur: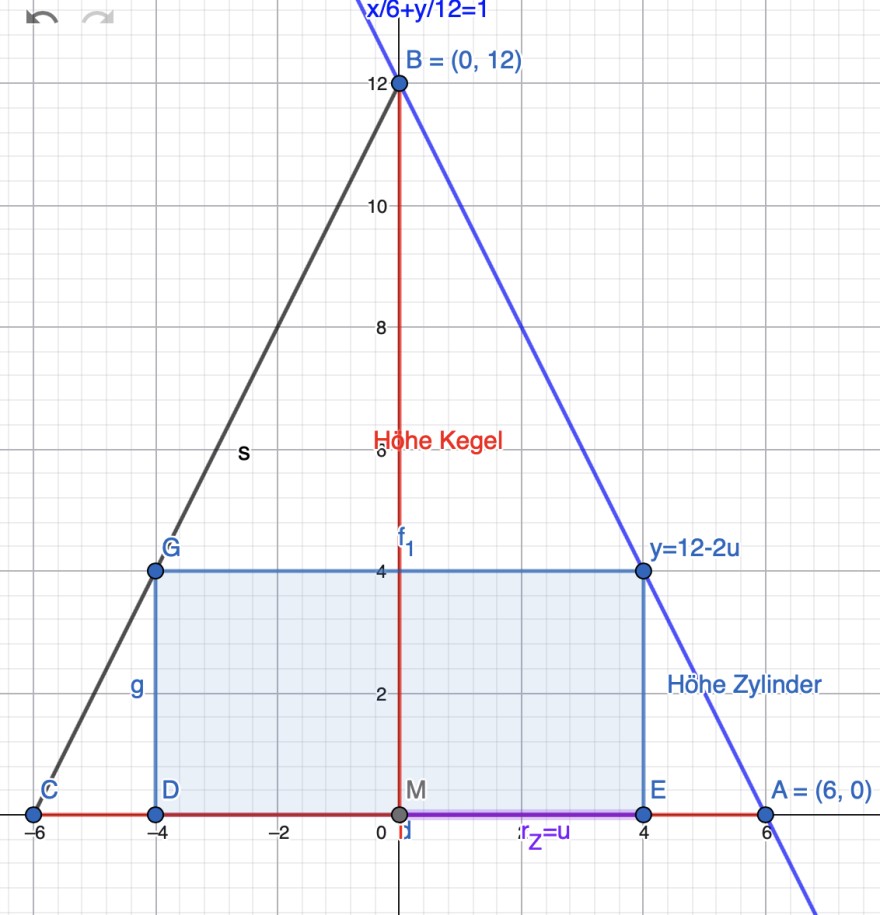

Die Geradengleichung durch A und B  ist durch die Achsenabschnittsform einer Geraden gewonnen worden.

Zielfunktion:

\( V(u,h_Z)=u^2π h_Z \) soll maximal werden.

Nebenbedingung:

\( h_z=12-2u \)

\( V(u)=u^2π (12-2u)=π(12u^2-2u^3) \)

\( V'(u)=π(24u-6u^2) \)

\( π(24u-6u^2)=0 \)

\( 24u-6u^2=0 \)

\( 4u-u^2=0 \) Satz vom Nullprodukt:

\( u(4-u)=0 \)

\( u_1=0 \) kommt nicht in Betracht (Den Nachweis hierzu erspare ich mir)

\( u_2=4 \)

Der Radius des Zylinders beträgt 4cm. Die Höhe ist 4cm.

Das maximale Volumen ist V = \( 64π cm^{3}\)