Question

Komplexe Zahlen: Realteil von z3 bestimmen

Aufgabe:

Gegeben seien die komplexen Zahlen \( z_{1}=-1-\sqrt{3} i, z_{2}=3 e^{i \frac{3}{4} \pi} \) und \( z_{3}=a-3 i=r e^{-i \frac{\pi}{4}} \) mit a, r ∈ ℝ und r ≥ 0.

Daraus soll sich berechnen lassen: \( \operatorname{Re}\left(z_{3}\right)=a=3 \).

Comments

Druckfehler in der letzten Zeile?

Das wäre vermutlich die erwartete Antwort.

---

Hier war das Originalbild: https://www.mathelounge.de/?qa=blob&qa_blobid=16177805449266122499

---

Danke. Über diesem Bild steht: Lösungen der Prüfungsklausur. D.h.

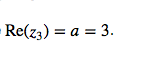
und all die andern Felder unterhalb der Fragestellungen sind die erwarteten Antworten, für die man vemutlich dann Teilpunkte bekommen hat.

Bitte das Bild der vollständigen Fragestellung wieder einblenden.

Gilt vermutlich bei allen Fragen von wiwi so. Bsp. https://www.mathelounge.de/646222/betragsungleichungen-intervalle

Kästchen ist das Ziel das Punkte gibt. Bitte entfernte Bilde nochmals kontrollieren. Sonst versteht die Nachwelt nicht mehr, warum in den Antworten etwas ausgerechnet wurde, das schon in der Fragestellung steht.

Habe die letzte Zeile nun in dieser Fragestellung hier anders eingeleitet.

Gleiches Problem wie erwähnt wohl bei vielen in den Editor übertragenen bisherigen Fragen von wiwi123.

Answer 1

r*e^(-i*pi/4) = r/√2 - i*r/√2

und wenn das gleich a - 3i  sein soll, dann muss

r/√2  = -3  sein , also

r =  -3√2   und damit    a = -3√2  /√2    =  -3 .

Comments

Warum sagt die lösung 3 ahhh da grösser gleich 0 ist oder

---

Ah ja, das hatte ich übersehen.

Answer 2

Du kannst z3 zeichnerisch bestimmen:

Achsen korrekt anschreiben.

z3 liegt im Schnittpunkt der beiden Geraden, z3 anschreiben.

Realteil von z3 ablesen. Re(z3) = 3