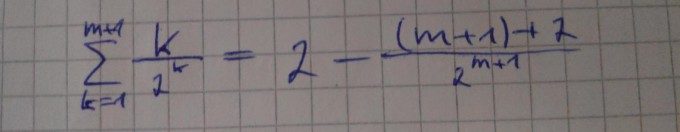Sitze grade an einer Vollständigen Induktions Aufgabe und komme an einer Stelle nicht weiter.
Kann man auf der rechten Seite die m+1 im Zähler mit der m+1 im Nenner Exponenten kürzen oder was genau muss ich hier machen?
Wäre sehr dankbar wenn mir einer helfen könnte :)