Berechne den Flächeninhalt A des Trapezes. b) Wie groß muss e sein ,damit sich A= 97 cm² ergibt?

Question

Aufgabe:

Answer 1

Hier war denke ich doch ein Fehler drin:

1/2·(e·2·√3/TAN(60°) + e·(6 - √3) + √((e·2·√6)^2 - (e·2·√3)^2) + e·(6 - √3))·e·2·√3 = 97 --> e = 2.000

Answer 2

Hallo

Aus tan(60) und Pythagoras die untere Seite ausrechnen, damit Fläche in Abhängigkeit von e, mit den92 cm^3 dann e.

Gruß lul

Comments

Vielen Dank lul meine kleine checkt es nicht und ich muss zugeben.das ich da schon vor der letzten Haltestelle ausgestiegen bin könntest du uns den rechenweg verallgemeinern das er bissle verständlicher wird

Answer 3

linkes Dreieck
untere Seite
tan ( 60 ) = e * 2 √ 3 / x
x = e * 2 √ 3 / tan ( 60 )
x = e * 2

Rechtes Dreieck ( Pythagoras )
( e * 2 * √ 6 ) ^2 = ( e * 2 * √ 3 )^2 + y^2
y = √ [ ( e * 2 * √ 6 ) ^2 - ( e * 2 * √ 3 )^2 ]
y = √ [ ( e^2  * 24  - 12 * e^2 ]
y = e * 3.4641

Trapez obere Seite
e * ( 6 - √ 3 )
untere Seite
x + e * ( 6 - √ 3 ) + y
e * 2 + e * ( 6 - √ 3 )+ e * 3.4641
Fläche Trapez
( obere + untere ) / 2 * höhe
( e * ( 6 - √ 3 ) + e * 2 + e * ( 6 - √ 3 )+ e * 3.4641 ) / 2
* e * 2 * √ 3

e = 2

Meine Lösung differiert etwas von der anderen Lösung.
Es ist aber schon spät und suche den Fehler
nicht mehr.

Comments

Deine Lösung ist richtig. Ich hatte bei mir oben noch einen Tippfehler gefunden und korrigiert.

Answer 4

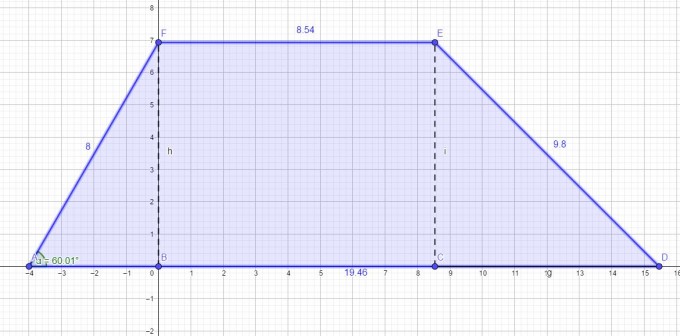
der Flächeninhalt eines Trapezes wird berechnet mit

$$\frac{g + a}{2}\cdot h\\$$

g entspricht den Strecke AD, a = e*(6-\( \sqrt{3} \) ) und h = e*2\( \sqrt{3} \)

g setzt sich zusammen aus den Strecken AB, BC (bekannt) und CD.

AB: ABF bilden ein rechtwinkliges Dreieck, in dem gilt:

$$tanα=\frac{\text{ Gegenkathete=Strecke AB }}{\text{ Ankathete }}$$

Wenn du die bekannten Größen einsetzt und nach AB auflöst, erhältst AB = 2e

Für das rechtwinklige Dreieck CDE gilt nach dem Satz des Pythagoras:

$$(CD)^2=(e2\sqrt{6})^2-(e2\sqrt{3})^2$$

Durch entsprechende Äquivalenzumformungen ergibt sich CD = 2e\( \sqrt{3} \)

Diese Ergebnisse setzt du für g und h in die Flächeninhaltesformel für das Trapez ein und setzt alles = 97. Dann nach e auflösen (e = 2).

Gruß, Silvia